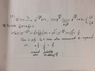You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Time dependent expectation value problems
- Thread starter BREAD
- Start date
AI Thread Summary
The discussion revolves around solving time-dependent expectation value problems in quantum mechanics, specifically regarding the state evolution under a Hamiltonian influenced by a magnetic field. Participants highlight that the initial state, which is not an eigenstate of the Hamiltonian, must be expressed in terms of the Hamiltonian's eigenstates for proper time evolution calculations. There is confusion about the probabilities calculated for measurement outcomes, with concerns raised about their validity as they should not exceed 1. The importance of normalization factors and the relationship between the energy eigenstates and the magnetic field direction are emphasized. The conversation concludes with a focus on calculating probabilities for subsequent measurements based on initial results.
Physics news on Phys.org
DrClaude
Mentor
- 8,477
- 5,693
You don't start the problem correctly. The ##|S_z = + \hbar/2 \rangle## state is not an eigenstate of the Hamiltonian, so after a time ##T_2##, the state of the system is not ##e^{-i E T_2 / \hbar} |S_z = + \hbar/2 \rangle##.
BREAD
- 50
- 0
DrClaude said:You don't start the problem correctly. The ##|S_z = + \hbar/2 \rangle## state is not an eigenstate of the Hamiltonian, so after a time ##T_2##, the state of the system is not ##e^{-i E T_2 / \hbar} |S_z = + \hbar/2 \rangle##.
--------------------------------------------------------------------------------------------------------------------------
H=-(e/mc)S * B , Sz and H differ just by a multiplicative constant, so they commute. The Sz eigenstates are also energy eigenstates.
(* I tried to solve it Sz not Sx by mistake)
Last edited:
DrClaude
Mentor
- 8,477
- 5,693
In which direction is the magnetic field?BREAD said:H=-(e/mc)S * B , Sz and H differ just by a multiplicative constant, so they commute. The Sz eigenstates are also energy eigenstates.
BREAD
- 50
- 0
In the problem, megnetic field is Bx direction.DrClaude said:In which direction is the magnetic field?
DrClaude
Mentor
- 8,477
- 5,693
So how can you rewrite ##\mathbf{S} \cdot \mathbf{B}##?BREAD said:In the problem, megnetic field is Bx direction.
BREAD
- 50
- 0
Sx * BDrClaude said:So how can you rewrite ##\mathbf{S} \cdot \mathbf{B}##?
BvU
Science Advisor
Homework Helper
- 16,208
- 4,925
So no commuting with ##{\bf S}_z## !
BREAD
- 50
- 0
Then how can i solve this problem. i would appreciate it if you can help me
DrClaude
Mentor
- 8,477
- 5,693
You have to express the initial state in terms of the eigenstates of the Hamiltonian.
BREAD
- 50
- 0
DrClaude said:You have to express the initial state in terms of the eigenstates of the Hamiltonian.
I think it is not. Sx and H have same eigenstates, so the initial state l+> is lSx+> + lSx->
DrClaude
Mentor
- 8,477
- 5,693
Don't forget the normalization factor.BREAD said:Sx and H have same eigenstates, so the initial state l+> is lSx+> + lSx->
But now that the state is expressed in terms of the eigenstates of the Hamiltonian, it should be easy to calculate the time evolution.
BREAD
- 50
- 0
DrClaude said:Don't forget the normalization factor.
But now that the state is expressed in terms of the eigenstates of the Hamiltonian, it should be easy to calculate the time evolution.
I think the answer is weird. These are the probability for Sz + , and 1-cos(T2/h)(E1-E2) for Sz -
So, the expectation value h/2(1+cos(T2/h)(E1-E2)) and -h/2(1-cos(T2/h)(E1-E2)) respectively
Last edited:
DrClaude
Mentor
- 8,477
- 5,693
Why? This is a very standard problem in QM and illustrates nicely the concept of precession.BREAD said:I think the answer is weird
BREAD
- 50
- 0
I replied the answer that i triedDrClaude said:Why? This is a very standard problem in QM and illustrates nicely the concept of precession.
DrClaude
Mentor
- 8,477
- 5,693
Ok, I had replied before you posted the solution.BREAD said:I replied the answer that i tried
There is a problem, as you can clearly see that the prbability you get ranges from 0 to 2. Check again how you calculate the absolute value squared.
BREAD
- 50
- 0
I got it, then how can i approach problem(b) i think the result of first measurement is same with (a)DrClaude said:Ok, I had replied before you posted the solution.
There is a problem, as you can clearly see that the prbability you get ranges from 0 to 2. Check again how you calculate the absolute value squared.
Last edited:
DrClaude
Mentor
- 8,477
- 5,693
The probability of measuring Sz = +ħ/2 is indeed given by the same equation, replacing T2 by T1. But you already know the measurement result, so you need to figure out what you get at T2.BREAD said:I got it, then how can i approach problem(b) i think the result of first measurement is same with (a)
By the way, you can simplify the result you get using explicit values for E1 and E2.
BREAD
- 50
- 0
DrClaude said:The probability of measuring Sz = +ħ/2 is indeed given by the same equation, replacing T2 by T1. But you already know the measurement result, so you need to figure out what you get at T2.
By the way, you can simplify the result you get using explicit values for E1 and E2.
Result of first measurement at T1 is the same with (a). I should have to get a probability of that state before i get a expectation value as i did in (a).
I think total result probability is probability(T1) * probability(T2)
Answer is quite complex, is it right??
BREAD
- 50
- 0
I changed it again.

Similar threads
- Replies
- 2
- Views
- 751
- Replies
- 5
- Views
- 2K
- Replies
- 14
- Views
- 3K
- Replies
- 4
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 7
- Views
- 5K
- Replies
- 31
- Views
- 4K
- Replies
- 5
- Views
- 2K
- Replies
- 15
- Views
- 6K
- Replies
- 1
- Views
- 1K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math