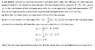kdlsw
- 16
- 0
For part a I have (H0-ω\hbarm)|nlm>, which I think the (H0-ω\hbarm) part is the eigenvalue of the Hamiltonian, also is the energies?
And mainly, I am not sure how to approach part b, the time variable is not in any of the states. I saw this in our lecture notes: ψ(r,t)=∑Cnψn(r) e-iEnt/\hbar. Do I simply add the e-iEnt/\hbar term after each ψ state? And then what? Please help me with this, thanks
And mainly, I am not sure how to approach part b, the time variable is not in any of the states. I saw this in our lecture notes: ψ(r,t)=∑Cnψn(r) e-iEnt/\hbar. Do I simply add the e-iEnt/\hbar term after each ψ state? And then what? Please help me with this, thanks