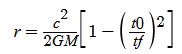Time dilatopause for black holes

[Feynstein100]

But as correctly stated above, the total energy depends only on $a$, no matter how large the excentricity $\epsilon$ with $0 \leq \epsilon<1$ is. Also the period doesn't depend on $\epsilon$, thanks to Kepler's 3rd Law
$$\frac{T^2}{a^3} = \frac{4 \pi^2}{G M} \simeq \frac{4 \pi^2}{G m_{\text{Sun}}}=\text{const}.$$

But a depends on eccentricity. It's the distance from the focus to the centre of the ellipse. The more eccentric the ellipse, the farther away the centre is from the focus and thus the greater the semimajor axis, right?

Ah okay as long as the endpoints/foci don't change, the eccentricity doesn't affect a. But that's not the image I had in mind. I meant stretching the ellipse outward until a is as large as we need.

 

[vanhees71]

$a$ is the major semiaxis of the ellipse, $e=\epsilon a$ is the excentricity ($\epsilon \in [0,1[$).

 

[Feynstein100]

What about them? They have to have at the surface larger than the minimum I gave in post #9, and you can calculate what the time dilation is for that. In fact I already gave an example in post #9.

Okay so as an example I'm taking the closest neutron star to earth, RX J1856.5−3754, which lies at a distance of ~400 light years according to Wikipedia.

The equation for gravitational time dilation is:

For a t0/tf ratio of 1/10, the distance to orbit is given by

The mass of the star is 1.79 * 10^30 kg. Plugging this into the formula,
r = 2685.4 m

Approximately 3 km above the surface of the neutron star. This might be a little too close for comfort but that's only because our neutron star wasn't very massive. From the equation, we can see that the more massive the star, the farther away we can orbit it for the same dilation factor.

Although, I haven't considered the speed dilation. At that distance, we could probably get more bang for our buck from the orbital velocity alone. For this purpose, both speed and gravity dilations work in our favor and add up, instead of cancelling out. So what we actually need is a formula for the combined time dilation from both speed and gravity. That is beyond my capabilities.

Also, the star has almost the same mass as the sun, which means the same calculation would apply to the sun as well. With the caveat being that orbiting the sun 3 km above its surface is not feasible with current technology. But damn, I didn't think we could get so much gravitational time dilation just from our sun. Huh.

 

[PeterDonis]

Approximately 3 km above the surface of the neutron star.

No. The formula you used is for the Schwarzschild radial coordinate, not the altitude above the star's surface.

If you look at the Wikipedia article [1], you will see that the radius of this star is estimated to be 19-41 km. The Schwarzschild $r$ coordinate is not exactly the same as radial distance, but it's close enough that an $r$ value of 3 km is well inside the surface of the neutron star--which means the formula you used is invalid, since it only works in the vacuum region outside the star.

Furthermore, you are completely ignoring what has been said in this thread about the limits on which values of $r$ permit free-fall orbits at all.

You also don't appear to have fully grasped the implications of the Buchdahl Theorem, which I mentioned in post #9, which puts limits on which values of $r$ are possible at the surface of a static object.

I strongly suggest that you take the time to consider fully these items before trying to make up any more scenarios.

https://en.wikipedia.org/wiki/RX_J1856.5−3754

 

[PeterDonis]

I didn't think we could get so much gravitational time dilation just from our sun.

You can't. The Schwarzschild $r$ coordinate at the Sun's surface is about $4.7 \times 10^5 \times GM / c^2$. Plug that into your formula and see what you get.

 

[Feynstein100]

No. The formula you used is for the Schwarzschild radial coordinate, not the altitude above the star's surface.

If you look at the Wikipedia article [1], you will see that the radius of this star is estimated to be 19-41 km. The Schwarzschild $r$ coordinate is not exactly the same as radial distance, but it's close enough that an $r$ value of 3 km is well inside the surface of the neutron star--which means the formula you used is invalid, since it only works in the vacuum region outside the star.

Furthermore, you are completely ignoring what has been said in this thread about the limits on which values of $r$ permit free-fall orbits at all.

You also don't appear to have fully grasped the implications of the Buchdahl Theorem, which I mentioned in post #9, which puts limits on which values of $r$ are possible at the surface of a static object.

I strongly suggest that you take the time to consider fully these items before trying to make up any more scenarios.

https://en.wikipedia.org/wiki/RX_J1856.5−3754

Oh, sorry. My bad

 

[PAllen]

It may have been said before in this thread, but I want to point out that at any distance above a spherical body that has a surface (I.e. not a BH), there is a (usually) forced circular orbit such that time signals exchange with the surface will show the clocks running at the same rate.