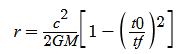Time dilatopause for black holes

[Feynstein100]

I was watching a video on GR by mathematician Matt Parker (he of the Parker Square) where he corrected some general misconceptions about GR. Most of the video wasn't anything special but there was one concept that stood out to me: the time-dilato-pause.

The idea behind it is quite simple: for any satellite orbiting a massive object, there are two time dilations at work: one from SR because of how fast it's moving in its orbit (speed dilation - SD) and one from GR because of its position inside a gravitational well (gravity dilation - GD). The time dilations are measured relative to the surface of the massive object.

SD and GD are in opposition to each other because SD tries to slow time down whereas GD tries to speed time up (again, relative to the surface). So the thinking goes that at some distance from the surface, SD and GD cancel each other out and the satellite experiences time at the same rate as the surface. This distance is termed the time-dilato-pause and someone calculated that it lies at a distance of 1.5R from the surface of the object, with R being the radius of said object. Actually, the original calculation was for the earth but I'm sure it can be generalized to any massive object.

Anyway, it ocurred to me that this was significant because it would allow the satellite to experience the same time dilation as on the surface of a massive body (relative to a farway stationary observer) without actually being on the surface. So naturally, my first thought was black holes. If there is indeed a time-dilato-pause at a distance of 1.5R from the event horizon, would a satellite orbiting at that distance experience the same time dilation as the event horizon, i.e. infinite time dilation relative to a faraway stationary observer?

The orbit would be well inside the innermost stable circular orbit (ISCO). However, provided we give it energy from the outside continuously, the satellite would be able to maintain the orbit and escape, basically experiencing what crossing the event horizon would be like without actually crossing it.
So is this actually possible or is there something that I haven't accounted for?

 

[Ibix]

I think you're a bit confused. You can certainly break time dilation down into a kinematic and a gravitational component, and compared to somebody at rest below you the two effects are opposite and can cancel out. I don't think there is a fixed ratio of radii at which it happens though. There is in a weak field approximation, but not in a full GR solution (I think - can check later).

You certainly cannot get the same time dilation as someone at the event horizon. That's primarily because time dilation can't be defined at the event horizon - the assumptions underlying the notion fail there. And the orbital speed needed for orbits at 1.5R is $c$ anyway, and the calculation Parker is doing is specifically for objects in freefall circular orbits compared to an observer at rest.

 

[PeroK]

So is this actually possible or is there something that I haven't accounted for?

The event horzon of a black hole is very different from the surface of a planet!

 

[Feynstein100]

I think you're a bit confused. You can certainly break time dilation down into a kinematic and a gravitational component, and compared to somebody at rest below you the two effects are opposite and can cancel out. I don't think there is a fixed ratio of radii at which it happens though. There is in a weak field approximation, but not in a full GR solution (I think - can check later).

You certainly cannot get the same time dilation as someone at the event horizon. That's primarily because time dilation can't be defined at the event horizon - the assumptions underlying the notion fail there. And the orbital speed needed for orbits at 1.5R is $c$ anyway, and the calculation Parker is doing is specifically for objects in freefall circular orbits compared to an observer at rest.

Actually, the calculation was not done by Parker but by someone called Kevin Brown. Anyway, he posted this equation and used binomial expansion to get a good approximation:

Parker said this was from GR so I assumed it was correct.
Hmm I thought time dilation was infinite at the event horizon. Isn't that why we can never see someone cross it?

And the orbital speed needed for orbits at 1.5R is anyway

Wait, I'm confused. Isn't that the condition for the event horizon?

 

[PeroK]

Wait, I'm confused. Isn't that the condition for the event horizon?

Are you confusing an objects's radius with its Schwarzschild radius?

 

[Feynstein100]

Are you confusing an objects's radius with its Schwarzschild radius?

No I meant that isn't the event horizon defined by the fact that to get out of it, you need to travel at c? So how can the same condition be true for somewhere outside the horizon? If it were, wouldn't the horizon just be there instead? Unless, getting out and orbiting are not the same?

 

[PeterDonis]

isn't the event horizon defined by the fact that to get out of it, you need to travel at c?

Heuristically, yes. But that is traveling at $c$ radially outward.

At $r = 3M$, an orbiting light ray is traveling at $c$ tangentially.

 

[PeroK]

No I meant that isn't the event horizon defined by the fact that to get out of it, you need to travel at c?

Not really. In the simplest terms it's defined by the Schwarzschild coordinate singularity. That means it's not legitimate to calculate anything in those coordinates at the surface itself. In particular, there is no calculation for gravitational time dilation for the event horizon. Whereas, a forced circular orbit at $1.5R$ has a valid calculation for the total time dilation (more precisely, the proper time of an orbit relative to Schwarzschild coordinates).

 

[PeterDonis]

If there is indeed a time-dilato-pause at a distance of 1.5R from the event horizon

There isn't, but not quite for the reasons that have been given. See below.

I don't think there is a fixed ratio of radii at which it happens though. There is in a weak field approximation, but not in a full GR solution (I think - can check later).

One should definitely check. See below.

Parker said this was from GR so I assumed it was correct.

It isn't, at least, not the way you are interpreting $R$ and $r$. See below.

a forced circular orbit at $1.5R$ has a valid calculation for the total time dilation

Not for a black hole, since such an orbit is null, not timelike. Similarly, a worldline "at the event horizon" is null, not timelike. The concept of "time dilation" does not apply to null worldlines.

This becomes immediately evident when one correctly interprets the first formula in the image in post #4: $R$ in that formula should be the Schwarzschild radial coordinate of the circular orbit, and $r$ should be the Schwarzschild radial coordinate of the surface of the massive object. With that interpretation, that formula is exact in GR. And it makes it obvious that, for a circular orbit at $R = 3M$ (the photon sphere, 1.5 times the horizon radius) around a black hole ($r = 2M$), the formula is undefined: both the numerator and denominator are zero. (On the OP's interpretation, with $R$ being the radial coordinate of the surface of the body, we would have $R = 2M$ and the quantity under the square root in the numerator would be negative: obviously wrong.) Furthermore, we can't plug in $r = 2M$ for any case whatever, since that makes the denominator zero--which of course it must since, as noted above, a worldline "at the event horizon" is null, not timelike.

If we consider a static object with $r > 2M$, however, and circular orbits at $R > 3M$, the formula is perfectly valid. Actually, by Buchdahl's Theorem, we must have $r > (9/4) M$ for a static massive object, so that is the range we should consider. And if we plug $R = (3/2) r$ into the first formula in the image in post #4, we see that it gives 1. So, for an object at the limiting value $r = (9/4) M$, a circular orbit at $R = (27/8) M$ would indeed have the same time dilation--and circular orbits inside that value of $R$ (and there is a finite range of them between there and $R = 3M$, the photon sphere) would have greater time dilation (clocks ticking slower) than an object on the surface of the object at $r = (9/4) M$.

(Note that all of this assumes that the massive object is not rotating. The actual Earth is, so the actual limit for orbits around the Earth as compared to objects at rest on the rotating Earth's surface is a bit different. I suggest leaving those complications aside for another time.)

 

[PeroK]

Not for a black hole, since such an orbit is null, not timelike.

An object can hover at $r = 3M$? And escape the black hole from there? But, not move laterally, keeping $r$ constant?

 

[Ibix]

An object can hover at $r = 3M$? And escape the black hole from there? But, not move laterally, keeping $r$ constant?

It can hover, escape, and move laterally. It can't orbit in free fall at that radius, though, because the required speed $\rightarrow c$ as you approach $3M$.

 

[PeroK]

It can hover, escape, and move laterally. It can't orbit in free fall at that radius, though, because the required speed $\rightarrow c$ as you approach $3M$.

I used "forced orbit" to distinguish it from free fall.

 

[PeterDonis]

An object can hover at $r = 3M$?

Sure, why not?

And escape the black hole from there?

Sure, by moving radially outward at escape velocity--or actually, moving at escape velocity at any angle to vertical that's less than 90 degrees.

But, not move laterally, keeping $r$ constant?

Not in free fall; to do that it would have to move on a null worldline.

One less frequently discussed property of Schwarzschild spacetime is that as $r$ decreases, the range of angles around vertical in which escape trajectories can point gets narrower. At $r = 3M$, it has narrowed to the point where tangential "escape trajectories" are null; and as $r \to 2M$, it narrows to the limiting case where even a worldline pointing exactly vertical--radially outward--is null, not timelike.

 

[PeterDonis]

I used "forced orbit" to distinguish it from free fall.

You can "orbit" at $r = 3M$ at an "orbital velocity" less than $c$ by hovering--using rocket power to maintain altitude.

 

[PeterDonis]

This Insights article might be relevant:

https://www.physicsforums.com/insights/centrifugal-force-reversal-near-black-hole/

 

[Ibix]

One should definitely check. See below.

I have checked and it does indeed work out, with the caveat you mention that $r$ doesn't mean radius in the conventional "distance to the center" sense because of the non-Euclidean nature of space in the Schwarzschild spacetime.

 

[PeterDonis]

the calculation was not done by Parker but by someone called Kevin Brown. Anyway, he posted this equation

Please provide a link.

 

[Feynstein100]

Please provide a link.

This should be it:
https://groups.google.com/g/sci.physics/c/2VrFGgiVPi8/m/F4KK_9MWrlMJ

 

[PeterDonis]

This should be it:
https://groups.google.com/g/sci.physics/c/2VrFGgiVPi8/m/F4KK_9MWrlMJ

Ok, thanks for the link.

Looking at this, I was correct that you had $R$ and $r$ backwards. $R$ is the Schwarzschild radial coordinate of the circular orbit, and $r$ is the Schwarzschild radial coordinate at the surface of the massive object. (Kevin Brown specifies the North Pole in order to remove the issues involved with the Earth's rotation.) But given that, there is no need whatever to expand in a power series in $M / r$, as Kevin Brown does. You can solve the equation exactly for the ratio $R / r$ that makes the time dilation ratio exactly $1$; the result is, as I said before, $R = 1.5 r$.

 

[Feynstein100]

Ok, thanks for the link.

Looking at this, I was correct that you had $R$ and $r$ backwards. $R$ is the Schwarzschild radial coordinate of the circular orbit, and $r$ is the Schwarzschild radial coordinate at the surface of the massive object. (Kevin Brown specifies the North Pole in order to remove the issues involved with the Earth's rotation.) But given that, there is no need whatever to expand in a power series in $M / r$, as Kevin Brown does. You can solve the equation exactly for the ratio $R / r$ that makes the time dilation ratio exactly $1$; the result is, as I said before, $R = 1.5 r$.

Wait, so is it applicable to black holes tho? If there's no need for the power series expansion then there's no approximation that only applies to weak gravitational fields, right?

 

[Ibix]

Wait, so is it applicable to black holes tho? If there's no need for the power series expansion then there's no approximation that only applies to weak gravitational fields, right?

It's exact, but only applicable outside the event horizon. Attempting to apply it to an observer at the horizon is self-contradictory.

 

[Feynstein100]

It's exact, but only applicable outside the event horizon. Attempting to apply it to an observer at the horizon is self-contradictory.

What about an observer at an infinitesimal distance away from the horizon? It seems to me that my original point still stands. We can have very high time dilation without actually needing to be at the horizon or needing to escape the gravitational well. It almost seems like a hack tbh. I wonder if this has any technological implications. For one, I think it would allow people to take a one-way trip to an arbitrary time in the future. I wouldn't mind being able to skip a few centuries ahead myself. The future is full of promise. Post-scarcity, immortality, technological singularity. If I had the choice, I'd see it all happen.

This isn't possible right now because we don't have the technology to travel at relativistic speeds. But if it were as simple as completing a few orbits around a black hole/nerutron star and then coming back out, it should be feasible with current technology.

 

[Ibix]

We can have very high time dilation without actually needing to be at the horizon or needing to escape the gravitational well.

Sure, but that's because the speed needed to orbit approaches $c$. And if you have the technology to do that then why bother with the black hole? Add to that that realistic holes have accretion discs, which are an enormous radiation and impact hazard.

 

[Feynstein100]

Sure, but that's because the speed needed to orbit approaches $c$. And if you have the technology to do that then why bother with the black hole? Add to that that realistic holes have accretion discs, which are an enormous radiation and impact hazard.

Damn, I hadn't thought of that. Orbits don't give extra energy. You need to have enough energy to be in the orbit in the first place. Otherwise you'll just fall in. Back to square one, it seems

Hang on. That's only true for circular orbits. Perhaps there's some wiggle room with elliptical orbits. After all, satellites in elliptical orbits only move at high velocities when they're very close to the object. Otherwise they move slowly.

Looks like my hunch was right. The energy in an elliptical orbit is given by

The more elliptical the orbit, the larger the semi major axis and the lower the energy needed to be in the orbit.

Of course, with the caveat being that the orbital period is now much longer but I think we can find a sweet spot for it.

And that you'll only experience relativistic velocities for a very short time but that's still better than not experiencing those velocities for any period of time with current technology

 

[Ibix]

Of course, with the caveat being that the orbital period is now much longer but I think we can find a sweet spot for it.

I'm pretty sure you can't, not with a Schwarzschild black hole. The more elliptical your orbit the cheaper it is, but the less time you spend at high speed deep in the gravity well and the more you spend at low speed high up in the well. We discussed a similar question here. If you can find an extremal Kerr black hole then you can do better, but it's not hugely better and you still have to get there from here.

 

[Feynstein100]

I'm pretty sure you can't, not with a Schwarzschild black hole. The more elliptical your orbit the cheaper it is, but the less time you spend at high speed deep in the gravity well and the more you spend at low speed high up in the well. We discussed a similar question here. If you can find an extremal Kerr black hole then you can do better, but it's not hugely better and you still have to get there from here.

There's still neutron stars

 

[PeterDonis]

is it applicable to black holes tho?

I already answered this in post #9, which explicitly gives the range of $r$ coordinates for the surface of the object for which it is applicable.

If there's no need for the power series expansion then there's no approximation that only applies to weak gravitational fields, right?

The very post of mine that you quoted answers this.

I'm pretty sure you can't, not with a Schwarzschild black hole.

I'm absolutely sure. See post #9.

if it were as simple as completing a few orbits around a black hole/nerutron star and then coming back out

There are no free-fall orbits inside $r = 3M$. And while there are timelike free-fall orbits for $3M < r < 6M$, they are unstable; a small perturbation either sends the object falling into the hole or escaping to infinity.

The only way to get very close to the horizon and stay there to take advantage of the extreme time dilation is to have enough rocket power to hover for an extended period. Our current rocket technology is nowhere near up to that.

The more elliptical the orbit, the larger the semi major axis and the lower the energy needed to be in the orbit.

What I said about free-fall orbits above applies to the periastron of elliptical orbits as well as to circular orbits. So no, this won't work either.

 

[Feynstein100]

There are no free-fall orbits inside . And while there are timelike free-fall orbits for , they are unstable; a small perturbation either sends the object falling into the hole or escaping to infinity.

Then how about an elliptical orbit with closest approach at r = 6M?

Also, neutron stars?

 

[PeterDonis]

how about an elliptical orbit with closest approach at r = 6M?

What about it? If you mean, how much time dilation would it have, it would have to be less than that of a circular orbit at $r = 6M$, and you can calculate that easily.

Also, neutron stars?

What about them? They have to have $r$ at the surface larger than the minimum I gave in post #9, and you can calculate what the time dilation is for that. In fact I already gave an example in post #9.

 

[vanhees71]

Damn, I hadn't thought of that. Orbits don't give extra energy. You need to have enough energy to be in the orbit in the first place. Otherwise you'll just fall in. Back to square one, it seems

Hang on. That's only true for circular orbits. Perhaps there's some wiggle room with elliptical orbits. After all, satellites in elliptical orbits only move at high velocities when they're very close to the object. Otherwise they move slowly.

Looks like my hunch was right. The energy in an elliptical orbit is given by
View attachment 321604
The more elliptical the orbit, the larger the semi major axis and the lower the energy needed to be in the orbit.

Of course, with the caveat being that the orbital period is now much longer but I think we can find a sweet spot for it.

And that you'll only experience relativistic velocities for a very short time but that's still better than not experiencing those velocities for any period of time with current technology

But as correctly stated above, the total energy depends only on $a$, no matter how large the excentricity $\epsilon$ with $0 \leq \epsilon<1$ is. Also the period doesn't depend on $\epsilon$, thanks to Kepler's 3rd Law
$$\frac{T^2}{a^3} = \frac{4 \pi^2}{G M} \simeq \frac{4 \pi^2}{G m_{\text{Sun}}}=\text{const}.$$

 

[Feynstein100]

But as correctly stated above, the total energy depends only on $a$, no matter how large the excentricity $\epsilon$ with $0 \leq \epsilon<1$ is. Also the period doesn't depend on $\epsilon$, thanks to Kepler's 3rd Law
$$\frac{T^2}{a^3} = \frac{4 \pi^2}{G M} \simeq \frac{4 \pi^2}{G m_{\text{Sun}}}=\text{const}.$$

But a depends on eccentricity. It's the distance from the focus to the centre of the ellipse. The more eccentric the ellipse, the farther away the centre is from the focus and thus the greater the semimajor axis, right?

Ah okay as long as the endpoints/foci don't change, the eccentricity doesn't affect a. But that's not the image I had in mind. I meant stretching the ellipse outward until a is as large as we need.

 

[vanhees71]

$a$ is the major semiaxis of the ellipse, $e=\epsilon a$ is the excentricity ($\epsilon \in [0,1[$).

 

[Feynstein100]

What about them? They have to have at the surface larger than the minimum I gave in post #9, and you can calculate what the time dilation is for that. In fact I already gave an example in post #9.

Okay so as an example I'm taking the closest neutron star to earth, RX J1856.5−3754, which lies at a distance of ~400 light years according to Wikipedia.

The equation for gravitational time dilation is:

For a t0/tf ratio of 1/10, the distance to orbit is given by

The mass of the star is 1.79 * 10^30 kg. Plugging this into the formula,
r = 2685.4 m

Approximately 3 km above the surface of the neutron star. This might be a little too close for comfort but that's only because our neutron star wasn't very massive. From the equation, we can see that the more massive the star, the farther away we can orbit it for the same dilation factor.

Although, I haven't considered the speed dilation. At that distance, we could probably get more bang for our buck from the orbital velocity alone. For this purpose, both speed and gravity dilations work in our favor and add up, instead of cancelling out. So what we actually need is a formula for the combined time dilation from both speed and gravity. That is beyond my capabilities.

Also, the star has almost the same mass as the sun, which means the same calculation would apply to the sun as well. With the caveat being that orbiting the sun 3 km above its surface is not feasible with current technology. But damn, I didn't think we could get so much gravitational time dilation just from our sun. Huh.

 

[PeterDonis]

Approximately 3 km above the surface of the neutron star.

No. The formula you used is for the Schwarzschild radial coordinate, not the altitude above the star's surface.

If you look at the Wikipedia article [1], you will see that the radius of this star is estimated to be 19-41 km. The Schwarzschild $r$ coordinate is not exactly the same as radial distance, but it's close enough that an $r$ value of 3 km is well inside the surface of the neutron star--which means the formula you used is invalid, since it only works in the vacuum region outside the star.

Furthermore, you are completely ignoring what has been said in this thread about the limits on which values of $r$ permit free-fall orbits at all.

You also don't appear to have fully grasped the implications of the Buchdahl Theorem, which I mentioned in post #9, which puts limits on which values of $r$ are possible at the surface of a static object.

I strongly suggest that you take the time to consider fully these items before trying to make up any more scenarios.

https://en.wikipedia.org/wiki/RX_J1856.5−3754

 

[PeterDonis]

I didn't think we could get so much gravitational time dilation just from our sun.

You can't. The Schwarzschild $r$ coordinate at the Sun's surface is about $4.7 \times 10^5 \times GM / c^2$. Plug that into your formula and see what you get.