Lisa...
- 189
- 0
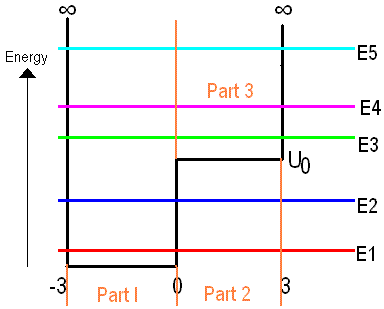
Is it true that, no matter what, the number of tops the wave functions of the energy levels in a one dimensional potential well (like the one shown below) have is the same as the number of that energy level? I.e. does in every well the wavefunction have 1 top in E1, 2 in E2, 3 in E3 etc?
Last edited:
 I just couldn't come up with the correct English word for it fast :D In the Netherlands we call them 'toppen' (that's why I wrote tops) or 'buiken' (which literally means bellies). Of course the word maxima is used too, but not quite often. Perhaps it has something to do with the (crown)prinses from Argentina whose name is Maxima...
I just couldn't come up with the correct English word for it fast :D In the Netherlands we call them 'toppen' (that's why I wrote tops) or 'buiken' (which literally means bellies). Of course the word maxima is used too, but not quite often. Perhaps it has something to do with the (crown)prinses from Argentina whose name is Maxima...