- #1
flfgw
- 11
- 0
Homework Statement
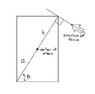
How much force is required to tip an object?
Given- It is a rectangular prism 1m tall, .5 m wide, 2m long.
The center of gravity is .75m from the ground vertically and otherwise centered.
The force can be applied wherever it is easiest to solve the problem.
Homework Equations
The Attempt at a Solution
I don't even know where to start on this one. In order to tip it i need to move the center of gravity over the rotation point. It would not move in a straight line however. It will follow the path of an arc. This is where I'm stumped. I am not to good with torque... does anyone know how to go about solving this?