Tipping point for box on incline

[anerky]

I'm wondering if anyone can help me with a problem that I came up with while trying to design an alarm-hourglass for myself..
I have math experience up to differential equations, but no real contact with physics, so I'm asking here.

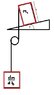
Given the situation in the picture: a mass suspended from a string (whose mass is being increased at a constant rate), wound around a pulley (whose frictional coefficient I have yet to test, but can be assumed arbitrary for now), and finally attached to the uppermost edge of a box of height h, with a square base of sides h/3. This box is on an inclined plane with an angle of theta from horizontal (friction prevents the box from moving).

Everything is fixed, except the increasing mass and the box.

At what point does the box reach the tipping point?
(I'll try to figure it out later just through geometry, intuition and the calculus, but would really appreciate some insight)

 

[CWatters]

As drawn I don't see how the pulley works. As the weight falls it appears the string attached to the block unwinds so it doesn't pull the block over.

Why not forget the pulley (initially) and just attach the weight to the corner of the block? I'll assume you have made that change...

Assuming it doesn't slip down the slope, at some point the block will start to rotate anticlockwise (pivot) about its bottom left hand corner. You can calculate the weight required for that by summing the moments (aka torques) about the left hand corner (the pivot). If we assume clockwise is positive then if the sum of the torques goes negative it will start to rotate anticlockwise.

There will be two torques to be evaluated each calculated as

Torque = force * perpendicular (horizontal) distance from the pivot point.

The two torques are..

Clockwise : The mass of the block * g * the horizontal distance between it's CoG and the pivot

Anti clockwise: The mass of the weight * g * the horizontal distance between the string and the pivot

Sum these taking care to use the correct sign. Work out when the sum goes negative.

Once the block starts to rotate I believe it will continue to tip because of the way the distances change (increasing on the left and reducing on the right, so the anticlockwise torque gets larger as it rotates).