gnits
- 137
- 46
- Homework Statement
- To calculate the centre of gravity of a spherical cap
- Relevant Equations
- comparison of moments
Could I please ask for help as to why I disagree with a book answer on the following question:

Answer given is book is $$\frac{1}{2}(a+b)$$
Here's my proposed method:
Prior to this question there is an example of a similar question:

And here is the answer:
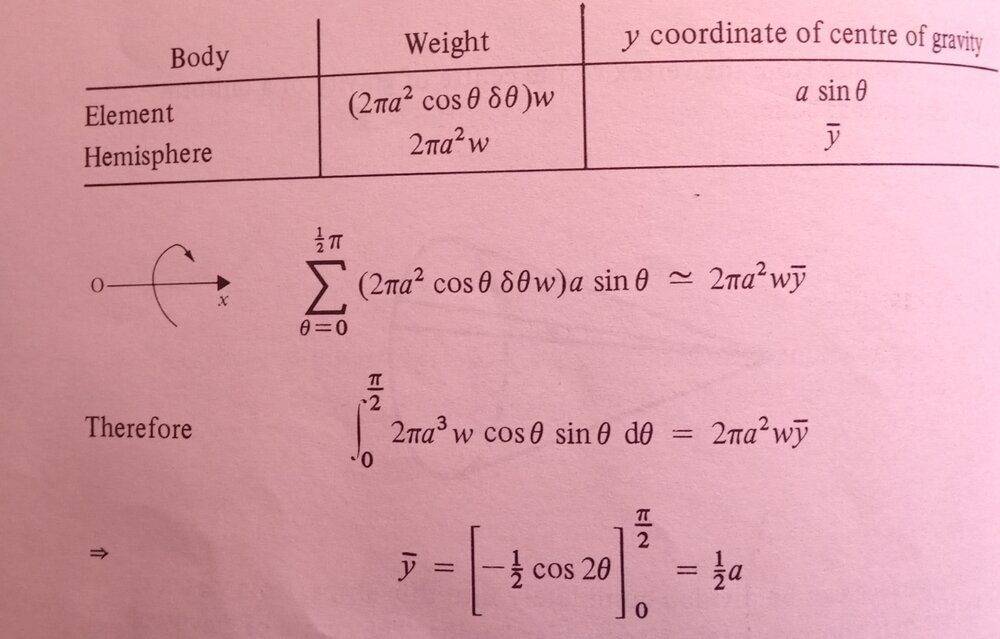
So, to solve my question I propose to solve the same integral but instead of the limits being $$0\,\,to\,\,\frac{\pi}{2}$$ I will use $$arcsin(b/a)\,\,to\,\,\frac{\pi}{2}$$
And for the area of the whole cap I will use the formula $$Area_{cap} = \pi(h^2+a^2)$$ where h is the height of the cap, so in my case h = a - b and so I have $$A_{cap} =\pi((a-b)^2+a^2)$$
Using Wolfram Alpha to solve the integral (for now, to see if I agree with book answer, will derive by hand if it works) have:
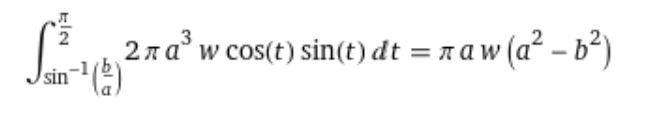
So equating moments, this would lead me to:
$$\pi\,a\,w\,(a^2-b^2)\,=\,\pi((a-b)^2+a^2)\,w\,\bar{x}$$
which gives:
$$\bar{x} = \frac{a(a^2+b^2)}{a^2+(a-b)^2}$$
Which is not the book answer.
Thanks for any help,
Mitch.
Answer given is book is $$\frac{1}{2}(a+b)$$
Here's my proposed method:
Prior to this question there is an example of a similar question:
And here is the answer:
So, to solve my question I propose to solve the same integral but instead of the limits being $$0\,\,to\,\,\frac{\pi}{2}$$ I will use $$arcsin(b/a)\,\,to\,\,\frac{\pi}{2}$$
And for the area of the whole cap I will use the formula $$Area_{cap} = \pi(h^2+a^2)$$ where h is the height of the cap, so in my case h = a - b and so I have $$A_{cap} =\pi((a-b)^2+a^2)$$
Using Wolfram Alpha to solve the integral (for now, to see if I agree with book answer, will derive by hand if it works) have:
So equating moments, this would lead me to:
$$\pi\,a\,w\,(a^2-b^2)\,=\,\pi((a-b)^2+a^2)\,w\,\bar{x}$$
which gives:
$$\bar{x} = \frac{a(a^2+b^2)}{a^2+(a-b)^2}$$
Which is not the book answer.
Thanks for any help,
Mitch.