carterwrangler
- 4
- 1
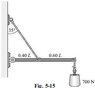
1. The uniform beam shown in figure 5-15 weighs 500 N and supports a 700 N load. Find the tension in tie rope and the force of the hinge of the beam.
The answer according to the book must be 2.9 kN as the tension in tie rope and 2.0 kN as the force of the hinge of the beam.
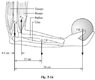
2. The arm shown in figure 5-16 supports a 4.0 kg sphere. The mass of the hand and and forearm together is 3.0 kg and its weight acts at a point 15 cm from the elbow. Determine the force exerted by the biceps muscle.
The answer according to the book is 0.13 kM which is the force exerted by the biceps muscle.
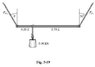
3. The uniform, 120 N board shown in figure 5-19 is supported by two ropes as shown. A 0.40 kN weight is suspended one quarter of the way from the left end. Find FT1 (force of tension 1) and FT2 (force of tension 2) and the angle made by the left rope.
The answer according to the book is 0.19 kN for FT1, 0.37 kN for FT2 and 14 degrees for the angle made by the left rope.
I don't know how the book got these answers, so I need a full explanation and solution for these problems. As much as possible, make it step by step.
Please help me! I'm an engineering student. I already looked at some examples, compared it and did the same process but it didn't match the book's answers.
The following figures/diagrams are uploaded. Any answers will be accepted as much as it is correct and very well explained. Thank you!
The answer according to the book must be 2.9 kN as the tension in tie rope and 2.0 kN as the force of the hinge of the beam.
2. The arm shown in figure 5-16 supports a 4.0 kg sphere. The mass of the hand and and forearm together is 3.0 kg and its weight acts at a point 15 cm from the elbow. Determine the force exerted by the biceps muscle.
The answer according to the book is 0.13 kM which is the force exerted by the biceps muscle.
3. The uniform, 120 N board shown in figure 5-19 is supported by two ropes as shown. A 0.40 kN weight is suspended one quarter of the way from the left end. Find FT1 (force of tension 1) and FT2 (force of tension 2) and the angle made by the left rope.
The answer according to the book is 0.19 kN for FT1, 0.37 kN for FT2 and 14 degrees for the angle made by the left rope.
I don't know how the book got these answers, so I need a full explanation and solution for these problems. As much as possible, make it step by step.
Please help me! I'm an engineering student. I already looked at some examples, compared it and did the same process but it didn't match the book's answers.
The following figures/diagrams are uploaded. Any answers will be accepted as much as it is correct and very well explained. Thank you!