Torque graph; finding angular velocity

[animanga008]

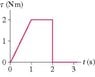
An object whose moment of inertia is 4.10 kg/m^2 experiences the torque shown in the graph attached.

What is the object's angular velocity at 2.70 s? Assume it starts from rest.

My main problem i think is how to read the graph. How should i interpret the graph?

What i would do first is find the angular acceleration by using...

aa = angular acceleration
t = torque
I = moment of inertia

aa= t/I

I would find the aa for three parts, the part where it is accelerating positively, when it is not increasing, and then when it decreases.

I would then use the aa for the equation while putting in the velocity...

w = angular velocity
T = time

w(f) = w(i) + aaT

 

[Nadialy]

i wish they would reply, i would like help with this also.

 

[rohanprabhu]

Well.. you have the Torque as a function of time. Break it up into 3 different functions, one for each of the time interval. At t=2, you can take it to be a part of either of the time interval, just make sure you include it in ONE and ONLY ONE of them.

Once you have \tau (t), divide it by I to get \alpha (t) = \frac{1}{I} \tau (t).

Then integrate it w.r.t to get the angular velocity in each of these intervals using proper limits. This might help you:

<br /> \Delta \omega = \int_{t_1}^{t_2} \alpha (t) dt<br />

Here, \Delta is used to denote that I'm computing the change in angular velocity since the given acceleration was applied. If the initial angular velocity was 0, you can take \Delta \omega = \omega. Once you have done that, you'll need to addup the angular velocities [or their differences rather] attained in each time interval. Do note that, no net torque doesn't mean zero angular velocity, it just means a zero change in angular velocity. Reply if you have any problems with this.

 

[tiny-tim]

Welcome to PF!

My main problem i think is how to read the graph. How should i interpret the graph?

Hi animanga008! Welcome to PF!

(btw, your original post was at 4am here in London, and just before midnight in New York … if you want a quick answer, you probably need to start a bit earlier!)

The torque is only in two parts.

(1) The torque increases steadily from t = 0 to 1, according to the formula tau = 2t (so, for example, at t = 1/4, tau = 1/2)

(2) The torque is then steady for one second.

After that, it disappears suddenly (in no time at all)!

 

[appelle moi]

Can anyone tell me why does the car engine have maximum power of e.g. 120 horsepower at 4200 revs per minute, and maximum torque of 250 Nm from 1400-2600 revs per minute?

The car seems to have the best acceleration in the range of the greatest torque (1400-2600 revs per minute), but not at maximum power (4200 revs per minute). What is the catch?

 

[rohanprabhu]

Can anyone tell me why does the car engine have maximum power of e.g. 120 horsepower at 4200 revs per minute, and maximum torque of 250 Nm from 1400-2600 revs per minute?

The car seems to have the best acceleration in the range of the greatest torque (1400-2600 revs per minute), but not at maximum power (4200 revs per minute). What is the catch?

Given the date of the post, I would suggest you start a new thread with your question. Please do not bump topics so old when the post content is not explicitly related to that of the op. Thank you.