Anode
- 2
- 0
Hi, I've been struggling on this homework problem for quite a few hours now and would really appreciate a pointing in the right direction. It's a fairly entertaining problem that I'm getting stuck on in several places.
1. Homework Statement
The problem goes:
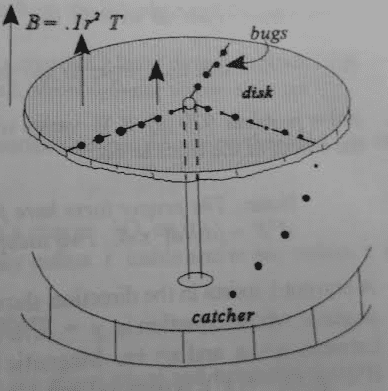
"An erratic engineer, who lives in a residence infested by small, fast bugs, conceives the device shown as a method of driving a disk. The bugs are taught to climb up the axle of the disk, emerge through a hole O at its center, and run radially outward at constant velocity. At the edge, the bugs fall off and drop into a tray. By means of a seat emf not shown, each bug acquires an electric positive charge as it ascends, and carries the charge with it as it runs across the disk. A magnetic field of flux density varying with radius according to B= 0.1r2 acts upward over the disk.
Suppose that 1000 bugs/sec emerge from O, each carrying charge +0.001 Coulomb, and move out radially. The radius of the disk is 0.5 meters.
a) Find the torque on the disk.
The given answer is 0.00156 n-m.
τ=rFsinθ
F=q(V x B)
τ=IBAsinθ
F=I(ℓ x B)
So, I've tried this several ways.
Here's the one I think is in the right direction:
I used both the equation for torque and the one for magnetic force.
So I get:
τ = r * qVB (since θ=90 by right hand rule)
τ = r * qV ∫ 0.1 r2 dr (and integrate from 0 to 0.5m)
τ = r * q * V * (0.5)3/3
τ = 0.5m * q * V * (0.5)3/3
Then, I have a problem. I'm fairly sure that q = 0.001C x 1000, but I could be wrong.
In any case, I'm stuck with V, and as far as I can see there's no way to find the velocity, since I'm given neither V nor time of travel of the bugs.
Am I missing something obvious? Thanks!
**diagram attached**
1. Homework Statement
The problem goes:
"An erratic engineer, who lives in a residence infested by small, fast bugs, conceives the device shown as a method of driving a disk. The bugs are taught to climb up the axle of the disk, emerge through a hole O at its center, and run radially outward at constant velocity. At the edge, the bugs fall off and drop into a tray. By means of a seat emf not shown, each bug acquires an electric positive charge as it ascends, and carries the charge with it as it runs across the disk. A magnetic field of flux density varying with radius according to B= 0.1r2 acts upward over the disk.
Suppose that 1000 bugs/sec emerge from O, each carrying charge +0.001 Coulomb, and move out radially. The radius of the disk is 0.5 meters.
a) Find the torque on the disk.
The given answer is 0.00156 n-m.
Homework Equations
τ=rFsinθ
F=q(V x B)
τ=IBAsinθ
F=I(ℓ x B)
The Attempt at a Solution
So, I've tried this several ways.
Here's the one I think is in the right direction:
I used both the equation for torque and the one for magnetic force.
So I get:
τ = r * qVB (since θ=90 by right hand rule)
τ = r * qV ∫ 0.1 r2 dr (and integrate from 0 to 0.5m)
τ = r * q * V * (0.5)3/3
τ = 0.5m * q * V * (0.5)3/3
Then, I have a problem. I'm fairly sure that q = 0.001C x 1000, but I could be wrong.
In any case, I'm stuck with V, and as far as I can see there's no way to find the velocity, since I'm given neither V nor time of travel of the bugs.
Am I missing something obvious? Thanks!
**diagram attached**