Torque on a square screw full with water

[Gh778]

Hi,

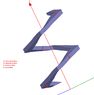
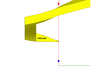
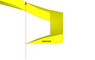
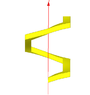
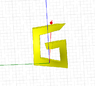
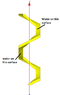
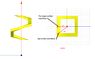
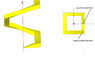
I would like to calculate the torque on a color square screw full with water like the drawing show. All grey screws don't move or turn, only color screws can turn (and so move up or down). Color screws are square (see top view for that). There is water between color screw and grey scew (gaskets are not visible ! ;) ), so like that the only faces can put forces are external and internal faces.

The problem for me, I see at each corner a small torque (because the altitude is not the same) but I don't find where this torque is cancel by another part of the screw. Can you help me ?

Maybe you need some others views, don't hesitate to tell.


Thanks :)

 

[Gh778]

This is like I see forces but maybe the weight is not full at bottom ? I'm drawing only a corner like that it's better for see where is another torque.

 

[Gh778]

I add some views of the thread.

I have cut 3D circular thread (first drawing) with 2 rectangular cuboids for obtain square thread (second and third drawings). Like that I'm sure the square thread can turn in the circular thread.

If you look at the square thread you can see a torque when the thread is in water due to external/internal surfaces. This torque is cancel by another torque with up/down surface. But it's easy to cancel this last torque if you put this square thread in a circular thread. So, another torque must cancel all torque but I don't find where. Maybe you can ?

Thanks

 

[Hassan2]

I' not sure I have understood the problem, but if you consider that the forces due to hydraulic pressure is normal to the surface ( which I'm sure you do), the problem is solved.

I think you can simplify the problem to a simple slab in the water. Wouldn't it be the same problem?

 

[Gh778]

Hi Hassan2 ;)

Yes, forces are normal to the surface, can you explain more I don't understand how ext and int surfaces give no torque ?

Up and down surfaces can be canceled so we rest with ext and int surfaces. Really, look at the drawings, you'll see a torque due to the corner. I don't think this 3D shape can be resume with a 2D shape.

thanks

 

[Hassan2]

The hydraulic force on any differential( infinitesimal)surface in any direction is equal to the force on the projection of the differential surface on the plane perpendicular to that direction.

Any differential surface at any point on the screw has a projection on the plane of the axis and r ( r being the vector from the axis to the point)being the distance from the axis). There is another differential surface on the other side of the plane the same projection on the plane, thus exerting equal forces in opposite directions.

This is true for any arbitrary shape.

 

[Hassan2]

About the torque on the screw in the figure, The force on the upper and lower sides are not equal. the torque the net is canceled by the net corner force.

 

[Gh778]

I'm ok with #6 message

#7: Yes a torque up/down cancel another ext/int, ok. But like it's a thread we can put it between 2 circular threads (show first drawing) and cancel up and down surfaces (for example with thin thickness of air with gaskets). We have only the external/internal torque. I don't know if you understand me ? Don't forget I cancel the up and down surface pressure easily and without energy.

 

[Hassan2]

Don't forget I cancel the up and down surface pressure easily and without energy.

In one of your figures, I see the words " up" and "down". My up and down surfaces are both sides of the thread separated by the thickness. The are not equal because they are like two parallel surfaces at different depth.

 

[Gh778]

The problem is, there are 2 thickness: up thickness and proof thickness. See the drawing below. Imagine air gap for up and down surfaces like that we sure there is no torque from these surfaces and we sure this cost nothing in energy if we turn in circular threads. But external and internal have a torque, for me, sure ;)

Drawing: look at "Z" axe

The are not equal because they are like two parallel surfaces at different depth.

It's not a problem to cancel the forces on these surfaces if we put small air gap (with gaskets) and put in a "sandwich" in 2 fixed circular threads. This cost nothing (in theory) about energy.

I add a drawing with a square thread in a "sandwich" of circular threads. Air gap at up and down surfaces.

 

[Hassan2]

Thanks for the explanations and the figure. I think I understands the problem now. In this simplified problem, no water touches the up and down and also internal surfaces. The problem becomes interesting and challenging now. Think of the proofs ( gaskets, fillers,..); They experience the same but opposite forces. If the gaskets are free, they transfer the force to the internal surfaces of the screw and cancel the forces on the screw. If there are rind connected like "another" screw, the forces cause a torque which tends to rotate the opposite direction the screw tends to rotate. Again no net torque.Added: Sorry in case of a rigid proof, my description may be incorrect.

 

[Gh778]

Thanks to you for your help ;) it's friendly

It's more difficult to think with the internal face without water because gaskets will be great with important surface. Or maybe I don't understand your explanations. Tell me ?

For my experience (no water at down and up surfaces but water at internal and external surfaces), the air gap could be like 1µm so the surface of the gasket is very small and this can't cancel the torque I see on internal/external surfaces. The weight can't be changed because internal/external surfaces are verticals.

 

[Hassan2]

Yes, but with water touching the internal faces too, again there is a net torque on the screw as you said before. But again the gaskets cancel the torque. If the gaskets thickness is much less than the screw thread, much of the forces on the thread is canceled by the forces on other side of the thread the remaining is canceled by the gaskets. If the thickness ratio is not small, again the number of gaskets must be large.

My problem now is with the case of the rigid gaskets fixed to the water container ( pipe). I have no explanation for this yet.

by the way, what software do you use for draw such figures?

 

[Hassan2]

You said that the gap is filled with air? it must be pressurized air, the same pressure as the water pressure. If so, it tells you where the cancelling force come from!

 

[Gh778]

You said that the gap is filled with air? it must be pressurized air, the same pressure as the water pressure. If so, it tells you where the cancelling force come from!

An air gap with air at pressure 1 bar for example, this air will apply the same force all along up and down surfaces, it's easy to do, and this cancel the pressure of water like that we can forget these surfaces (they have the same surface) and think with only external and internal surfaces. I use Maxwell (electromagnetic simulator) but I think you can do with Blender (free) but I don't know how.

but with water touching the internal faces too, again there is a net torque on the screw as you said before.

it's evidence that the external surface apply much torque than internal surface but need some calculations for be net.

If the gaskets thickness is much less than the screw thread,

When you think about that you imagine a square thread in a sandwich of 2 circular threads ? I don't understand.

If the thickness ratio is not small, again the number of gaskets must be large.

I don't understand what case you think. Don't forget the square thread will be turn, and this said it will move up (or down) and if water is not everywhere around, the water can (it depend of the torque) move down and we can lost energy like that.

My problem now is with the case of the rigid gaskets fixed to the water container ( pipe).

Could you send a drawing even with pen ? I don't understand.

 

[Hassan2]

Read post #14 please. There must be a pressure on the up and down forces otherwise water fills the narrow gaps. This pressure doesn't answer the question? As if the screw was in the water without any gasket.

 

[Gh778]

There must be a pressure on the up and down forces otherwise water fills the narrow gaps.

Not like you think, the gasket is only there for prevent water to fill the air gap, you can think with P=0 bar in the air gap. Sure water will put forces on surface of the gasket [because we have X bars in one side due to the water, and this change with altitude, and 0 bar in other side (air gap)] but the surface of the gasket can be so low that we can considered the torque = 0 on the gasket. In this case, I put thr square thread in a sandwich of 2 circular threads, it's very important, the gaskets don't have up and down surfaces, they have only external and internal surfaces but so small...

 

[Hassan2]

First of all, the problem is the same for any sort of screw thread, square of helical or even arbitrary shapes and asymmetric teeth. I think the problem is becoming more clear and more simple. Imagine the three scenarios:

1. No gasket at all, all surfaces are in touch with water. In this case the problem is solved and we agreed on it.

2. gasket fills the spaces fully and rigidly as if the whole is one object. again , the problem is solved. No mater if the object has tooth or blades. I guess you still have problem with this but it is solved for me. Narrow or thick doesn't matter.

3. The gasket is there but it is not stuck to to the surfaces.Water will enter in between and it becomes case 1 or a combination of 1 and 2.

I have an analysis in my mind and if I can convey it to you, you would have no problem with the small thickness of the gasket. I try it here:

The net torque on the screw due to screw surface only, depends on the ratio of the filler( gasket) thickness to the screw thread thickness. When the ratio is small, this means most of the force on the screw surfaces is canceled with their opposite forces on the other side where the water has the same depth. In fact at any point on the screw surface, if you can connect a line throw the screw thread to the other side with the same height, WITHOUT passing through the gasket, the force on that point is canceled. If the ratio is small, more points of the surface are like that. If the ratio is not small but the thickness is small, this means we have almost as much gasket surface as thread surface ( external surface). The total torques are not negligible.

I have made a poor drawing to show how a portion of the forces cancel each other. In the figure, the black arrows canceled by the forces on the other side of the thread. The red ones are not because the gasket/gap is between them.

 

[Gh778]

First of all, the problem is the same for any sort of screw thread, square of helical or even arbitrary shapes and asymmetric teeth

Ok but I would like to understand this particular problem in details ;)

I put two 3D drawings:

1/ a zoom of the bottom of the thread (yellow), we can see the difference of altitude of the thread and this show there is a torque with external/internal surfaces,
2/a zoom of the thread in sandwich with anothers fixed thread. I put the gasket extremely thin 1µm between yellow and grey threads. This don't cost energy. And inside (the volume create by gaskets which is between up/down surface and grey surface) there is no water only air.

I have questions:

a/ are you agreed with the torque with only 2 surfaces external/internal (don't think at another surfaces) ?
b/ Why do you think the torque is proportional with the thin of the torque ? The thickness of the square thread don't change with the thickness of the gasket.
c/ orange color of your drawing is gasket for you ? Because for me not at all. See for that the zoom.

Thanks for your help ;)

 

[Gh778]

I have draw new thread like that no problem with part of the axe Z.
Maybe it's more easy to see where I see a torque ?

 

[Hassan2]

You're welcome,
Thanks for your patience. I often forget what you have already explained to me. In in my posts, replace gasket by "fixed threads". That's fine

answers:

a. Yes, in your figure, where the gasket has sealed the space, hydraulic force is on external and internal forces only. But I see another force there. That is the force on the up and low surfaces of the "fixed thread. The net torque on the turning thread due to direct hydraulic pressure is non-zero. The force on the upper and lower surfaces of the fixed thread causes an opposite torque and they are canceled out. Just like when the turning and the fixed threads were welded to one another.

b/ Since I had confused the gasket and the fixed thread, I change my statement now. It depends on the ration between the thickness of the fixed thread and the turning thread which seems to be near one. I tried to show it in the figure. Just imagine a very thick turning thread with a thin fixed thread, then for most of the surfaces of the turning thread, the there is another point on the the forces on both sides. Although we don't need this argument anymore, a reason is that when the distance between fixed threads is high, a higher portion of the turning thread is exposed to two-sided hydraulic pressure.

c/ Sorry for the mistake, the orange is the fixed thread. The gaskets are ignored.

The fact behind all the discussion is that the fixed and turning threads are being pressed against each other by water pressure, and this is very usual and causes no net torque.

 

[Gh778]

many thanks ;)

don't mind about your confusing it's nothing

b/ I'm ok

a/ I had another drawing for show the bottom and start the thread new way because in my last drawings there is a small difference of surface internal/external. I'm ok that this torque is canceled with up/down surfaces. But I can cancel the up/down surface by adding air gap with near 0 pressure and this will cost 0 in energy. Do you understand my problem ?

 

[Hassan2]

I'm ok that this torque is canceled with up/down surfaces.

I meant the up and down surfaces of the fixed thread where it is in touch with water. Since the turning thread is square, some area of the up and low surfaces of the fixed thread feels the water pressure directly and that causes an opposite torque. If both threads were circular of course we didn't have the problem at the first place because the forces would be normal and cause no torque.

 

[Gh778]

I meant the up and down surfaces of the fixed thread where it is in touch with water.

no, ok all the system is in water, all surfaces of fixed threads are in contact with water except where the square thread is. Like they are fixed thread I don't care about the torque on these threads.

Since the turning thread is square, some area of the up and low surfaces of the fixed thread feels the water pressure directly

no, because the square thread is in fact a circular thread which I deleted some areas with rectangle cuboid. The up/down surface of square thread is always in contact with grey surface

Usually, the difference of surfaces at bottom must compensate the torque but they can't because I can choose this difference more in front of the axe. Another manner of thinking, it's increasing the radius of the thread and don't change thicknesses of square thread, this will change the torque but not at bottom. I think I will calculate this.

Another problem is if the pitch of the thread increase the difference at bottom section decrease but the torque not.

 

[Gh778]

Sure the difference of the surface need calculations. I will try later.

For now, I have another case with this square thread.
Imagine this new case:

1/ All system in air, not in water
2/ An empty square thread with air inside at P=0 (it's a theoretical study), Weight of this square thread = 0 Newton (theorical)
3/ Put the square thread in sandwich between two fixed circular threads
4/ Put water on up and down surfaces only. Extremely thin thickness of water (1µm for example), in theory the weight of water can extremely low (for simplify the study, imagine the weight of water = 0 Newton), I want the weight of water very low like that I don't think about the energy need for move up or down the water.

I want the weight of square thread and water very low like that I don't think about the energy need for move up or down the water. Sure in practise there is a small weight. In the drawing the radius is a mean radius.Now:

a/ up surface = down surface, by building
b/ total up force due to the pressure of water = total down force, by building
c/ the torque (for me) is not to 0 because there is a phase angle for the radius of application of the force, and the force is lower with altitude (pressure of water). See the drawing for that.

I hope you can understand my problem

Thanks for your help Hassan2 ;) and have a good day

 

[Hassan2]

Thanks GH778,

Before we make the problem more complicated, let's discuss on a simple problem in the figure I have attached. This is to show that the forces and torques on the the fixed parts must be considered too.

In the figure, the gray cylinder is fixed to the axes. The blue piston can displace freely in the cylinder. There is air in the gray cylinder so the piston doesn't touch the button. Now, can we consider the torque due to the blue piston only and conclude that there a net torque? Of course no. For the screw problem also we can't ignore the torque on the stationary parts.

 

[Gh778]

I'm ok with your drawing and torque. But take a moment for read and understand my last message because it's not more complicated, it's very easy to understand. Have you understand the phase angle ?

 

[Hassan2]

Thanks. That is simpler.

b/ I don't agree. it depends on the pressure profile. If the upper and lower water films are connected ( for example both are connected to the same source from the to), then the total forces on the lower surface is higher which causes a buoyancy force upward.

c/ Again if the water films are not connected ( i.e they don't have the same pressure at the same depth), there could be a net torque. The thread becomes a turbine then. In case of connected water, at any point the torque is counter balanced by an opposite torque in the other side. No matter the point is on the corner of in the middle.

Water's head doesn't depend on the mass of the water but on its height, density and on the gravity. So, the problem is equal to having the space between the threads filled with water.

 

[Gh778]

b/ no, they are not connected

c/ I see a torque, but it's not possible in fact, because we don't give energy to the system but we can recover energy. I thought about the weight but the thread can be with weight near 0 N because we use pressure of water (it depend of altitude) not the weight of water.

Note: the space between square thread and grey thread is for example at 1µm but the surface is equal at the up (or down) surface so the torque is high on the up surface (or down). Sure the anlge phase is not very important torque but it seems to exist. I don't find where's the problem ?

 

[Hassan2]

Torque without angular velocity gives no energy/work. If the thread starts turning, The pressure balance will change and we need to to do work to keep the pressures the same.

The phase angles are eventually irrelevant because the torques are canceled at point. The torque on far points are canceled by the opposite torque on the point. Same goes with near points.

 

[Gh778]

If the thread starts turning, The pressure balance will change

I don't understand this point. The thread is always the same, the water up and down is always here. Can you explain ? If the thread starts turning, it has always water up and down.

The phase angles are eventually irrelevant because the torques are canceled at point

Have you see the pressure on the drawing, it decrease like the angle increase and this prevent to cancel last torque. Example, we have 10 at start, after we have -9, after +8 after -7 etc. The sum can't be to 0 I think.

 

[Hassan2]

Can you please explain how the films are kept there? Each film has two sides, one side is in touch with the thread, how about the other side? in touch with a stationary part?

 

[Gh778]

The film is film of water I supposed ? If yes, you're right the film of water has one side on the square thread and one side on the fixed thread (up and down). For me a torque is on the square thread and another torque on fixed threads. But like the square thread turn only, this give energy I suppose.

 

[Hassan2]

How can such a thread rotate? The fixed thread has locked it. As soon as it starts to move it is stopped by the upper thread.

 

[Gh778]

Not at all, the square thread is a thread building from a circular thread:

1/ I draw a circular thread
2/ I substract a rectangle cuboid
3/ I take intersect with a bigger rectangle cuboid

When I say square thread, it's at the top view, but in fact at origin it's a circular thread which can turn in a circular thread (sure with the good pitch). I only deleted parts for have a thread like I study. And all square thread I drawing in this topic come from circular shape and this method.

I put an example of equation for the torque (it's not a real case only an example for see the next torque can't cancel the last)

I hope you can understand ;)

 

[Hassan2]

Sorry, I had no problem with the shape of the thread but I was assuming the system to be a screw pump. In a screw pump, the thread turns without axial displacement. By turning, it displaces the fluid in the space between the thread, so no fixed thread can be there.

In case of a screw with degree of freedom in axial direction, We can have fixed thread then. Something became clear now. The upward force ( buoyancy farce) is converted to torque through the reaction of the fixed thread on the turning thread. It's also compatible with common sense too. For example a screw made of a low density material tends to pop up when placed in water. If its threads face an obstacle with low friction, it starts turning. Perhaps this is what you were trying to prove all along. If so, congratulations! But the conservation of energy is still held. Energy was spent to push the screw inside water.

 

[Gh778]

Sorry, I had no problem with the shape of the thread but I was assuming the system to be a screw pump. In a screw pump, the thread turns without axial displacement. By turning, it displaces the fluid in the space between the thread, so no fixed thread can be there.

Yes, here the grey threads don't turn, in contrary the square thread turn and so move up or down.

Perhaps this is what you were trying to prove all along.

no, no, no ! I'm looking for the truth, I know it's not possible, I just want to see where the another torque is but I don't know where it is.

The upward force ( buoyancy farce) is converted to torque through the reaction of the fixed thread on the turning thread.

don't forget:

1/ the up surface = down surface
2/ water at up is not connected to down surface, so the up force = down force
3/ In standar system we must give energy for put air in water for example, here the energy can be near 0 so I'm sure there is another torque somewhere

Energy was spent to push the screw inside water.

I know I have changed the system, sorry for that, at first we put thread in water (thread that can be of density like water), but in the second system I put all the system in air, I put only film water at up and down surfaces. In one case like another I don't need energy (in theory). In the first case I takeoff very few water in second I put very few water, this need very low energy compared to the angle phase of torque.

Maybe you can see where is the problem, thanks for your patience ;)

 

[Hassan2]

If instead of water, we had pressurized air in the gaps, both pressures the same, would your calculation still yield a net torque ?
Also in one of the figures I see a plot. What is the horizontal axis?

 

[Gh778]

If instead of water, we had pressurized air in the gaps, both pressures the same, would your calculation still yield a net torque ?

No torque because pressure don't decrease with altitude. I'm agree with that. It's the angle phase of the radius which give problem for me.

The plot (the integration ?) it's an example for see if the pressure decrease with altitude (100-x) the angle phase of the radius (sin(x)-sin(x-3.14)) the sum of the product is not 0. If you do the calcul with 100 not (100-x) you'll obtain 0 or near (it depend where you stop the integration).

 

[Hassan2]

Are you sure that sin(x-3.14) is correct. I guess it should be sin(3.14-x)!

 

[Gh778]

sin(3.14-x)=sin(x) I think so if you look at the phase angle you can see the courbes have pi phase. Sure if you integrate (sin(x)-sin(x)) * (100 -x) this give 0, ok. But the radius is dephasing.

 

[Hassan2]

Yes they are equal!. But for a constant pressure, ( 100 ), the torque should become zero without integration. The two sines must cancel out. I don't know how the sines came into your equation, but check it once again.

 

[Gh778]

See the drawing, sine is for simulate up radius and down radius. I have put sine for example of a phase angle, it's not the true mean radius by the real pressure. It's only for show the next torque can't cancel the last (it's logical but with an equation we can see if it's true or not). Maybe the curves are not exactly sine but there is a phase angle. What I'm sure is the radius change and the pressure in the same time and the radius of down surface is dephasing with up surface. I would like to have the true equations of the surface for do calculations but it's difficult I need time for that. I'm happy for your help :)

 

[Gh778]

I have think about the equation of the radius. it's R/cos(x) from 0 to π/4 and √2*R*cos(x) from π/4 to π/2 (repeat if for 2π), sure it depend where you're starting the pitch. It's a function of sin (or cos) and it's like that I can draw the radius like the drawing show above. For the integration, I can put the cos or sine I think. Sure, I need the complete calculations but it's logical, no ? I don't know where is another torque or maybe something else is wrong.

Have a good day

Edit: I have choose (sin(x)-sin(x-3.14))*(100-x) it's the worst case, if the phase angle is lower 1 rd for example, we have (sin(x)-sin(x-1))*(100-x), the result is 45 but not to 0.

 

[Hassan2]

I think you are wasting your energy and time by integrating and also considering different surfaces and radii.

Cut the thread with planes perpendicular to the axis. Think of the in-plane component of the force which causes toque. The torque is canceled by an opposing torque due to the same film of water. To make it simple, assume the thread to be very thick. I think the opposing torque must be found there not in the lower film. Can you make a cut of the thread and film by your software and show it in 2-dimensional space?

 

[Gh778]

I join two different square threads with a bottom view (it's like a cut view because the thread is cut perpendiculary to the axis). I can't exactly show the film with my software, but why it's important (don't forget the film can be like 1µm of thickness) ? Here we can see r2>r1, don't forget the slope is always the same all along the thread because it's a circular thread at start. Ask me if you want more views of the thread. I put 2 examples with differents phase angle.

 

[Hassan2]

Thanks for the figures. We should not ignore the side force, both inside and outside. There must be a pressure on both sides, other wise the water gets out. The side pressure cause forces. If the inner surface was circular/cylindrical, would cause no torque, For a square threads they cause torque. Do you agree with me?

For simplicity, I have assumed a part of the thread spanning 90 degrees only. Also the lower surface is assumed to be flat, a plane parallel to xy plane ( the thickness of the thread increasing by angle), so it causes no torque. Both upper and lower surfaces are under equal constant pressure ( pressurized gas). As we know, the net torque must be zero. According to your calculation, There is a large torque because the lower one causes no torque to cancel it out. Now think about side forces and their contribution to the torque.

 

[Gh778]

But the thread is not full in water. It's the second case I study, I put only film of water only to up and down surface, not external/internal surfaces. There is only 2 surfaces in contact with water up and down only.

 

[Hassan2]

1. In the first case if study, when you removed some part of the thread to make it square you should not ignore the force due to those removed parts.

2. In the second case, the water can't remain there without some side pressure. What contains the water on from the sides? When you assume water ( without flowing) there, You are assuming a side pressure too.

3. Seems you had no problem with the circular thread at the beginning. But after you cut it by the cuboid, You found a contradiction. When we remove, we should consider the forces due to the removed parts.

 

[Gh778]

2. In the second case, the water can't remain there without some side pressure. What contains the water on from the sides? When you assume water ( without flowing) there, You are assuming a side pressure too.

Gaskets remain water. Torque from gaskets ? So small if the film is 1µm or less I think we can consider like 0.

3. Seems you had no problem with the circular thread at the beginning. But after you cut it by the cuboid, You found a contradiction. When we remove, we should consider the forces due to the removed parts.

Yes, I'm finding the solution of the problem;