Torque on a square screw full with water

[Gh778]

does the angle depends on r?

for me yes, you can't see the drawing ?

 

[Gh778]

I'm working about the angle and the torque.

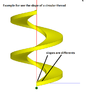
The equation of a helicoid is:

x=v*cos(u)
y=v*sin(u)
z=u

With u and v reals, v is the radius, u is the altitude

Perpendicular vector or normal vector (n) to the surface is :

n = v1 x v2 with "x" cross product and v1, v2 two vectors of the tangent plane

Vector=(v*cos(u), v*sin(u), u)

v1=dVector/du=(-v*sin(u), v*cos(u), 1)
v2=dVector/dv=(cos(u, sin(u), 0)

n = v1 x v2 = (sin(u), -cos(u), v)

We can see the angle of the perpendicular vector to the surface, it's like we said before.

I'm trying to do the full torque around Z axis.

 

[Hassan2]

Thanks for the equations. It like the formula of normals. I didn't know this formula and I usually use gradient method. For parametric curves your method is easier. Now I can imagine what surface the screw has.

In order to calculate the total torque, you need to use equations of equilibrium too.

 

[Gh778]

For you, these equations validate the torque dM=r*P*de*dl*sin(θ) ?

 

[Hassan2]

what are de and dl?

 

[Gh778]

dA=de*dl the small area

 

[Hassan2]

That's correct. But you can test your formula on a sphere in the water. the sphere haszero mass and is connected to a horizontal axis with a mass-less bar. the torque is expected to become ro*g*V*L , where the V is the volume of the sphere, ro is the density of water, and L is the distance from the center to the axis.

 

[Gh778]

It's very difficult to have the equation of the square thread for have the torque. I decided to find it with numerical solution. Here it's the program in C language. I hope you know this language but it's not difficult to read it with mathematical equations. I have take pressure in bar in local torque but done total torque in Pa.

The start of the helicoid is done by "d". If d=0 we have 214500 Nm but if d=-0.45 rd we have 217000 Nm for the total torque. Maybe something is wrong in my program or maybe there is a torque like I said before, in this case I don't find the contrary torque.#include <stdio.h>
#include <math.h>
#include <stdio.h>

int main(void)
{
double x=0.0,y=0.0,z=0.0; // each point of the circular thread, I use circular thread and after select only points which are on the square thread
double u=0.0,v=0.0; // u=altitude, v=radius
double a=0.0; // angle
double torque=0.0; // local torque
double torqueT=0.0; // total torque
double pas=0.001; // step for integration
double pi=3.1415927;
double vLimit=2*pi, uLimit=2*pi; // limit of integration, in meters
double c1=3, c2=4; // limit of the square thread in meters
double d=-0; // angle start for the helicoid

do
{
do
{
//calculation of each point of the helicoid
x=v*cos(u-d);
y=v*sin(u-d);
z=u;

// select only point for have the square thread
if( (x>c1 && x<c2 && y<c2 && y>-c2) || (x<-c1 && x>-c2 && y<c2 && y>-c2) || (y>c1 && y<c2 && x<c2 && x>-c2) || (y<-c1 && y>-c2 && x<c2 && x>-c2) )
{
a=atan(uLimit/2/pi/v);
torque=v*(uLimit-u)/10.0*sin(a)*pas*pas; // Here the pressure is (uLimit-u)/10.0 in bar //// pas*pas = surface
torqueT+=torque;
/*
// print part result
printf("\nu=%f, v=%f", u,v);
printf("\nx=%f, y=%f, z=%f",x,y,z);
printf("\na=%f, couple=%f",a, torque);
printf("\nT=%f", torqueT);
system("pause");
*/
}
v+=pas; // increase step of integration
}while(v<vLimit);
v=0;
u+=pas; // increase step for integration
}while(u<uLimit);

printf("The total torque is: %f",torqueT*100000.0); // * 100000 for pass from bar to Pa unity
}

 

[Hassan2]

I have checked the code by the result only and I think there is a problem in your code. I think if we make uLimit half, the torque becomes half too. in your code the relation is not linear. Also I have doubt about your differential volume. I don't think it simply becomes the product of the differential change in u and v. for example on the surface of a cylinder, ds=rdrdθ . For the helocoid, you can find a formula by relating the surface element to its projection on xy plane.

 

[Gh778]

For the helocoid, you can find a formula by relating the surface element to its projection on xy plane.

How can I do ?

Like the drawing ? maybe sin(a)+cos(a) ?

.

 

[Hassan2]

Imagine a differential surface of the surface between u and u+du, and v and v+dv. On the xy plane the projection of area is vdvdu ( as in polar coordinate). The surface on xy plane then becomes:

ds_{xy}= ds cos\theta

where θ is the angle between the normal and Z axis. so

ds= \frac{vdvdu}{cos\theta}

 

[Hassan2]

How can I do ?

Like the drawing ? maybe sin(a)+cos(a) ?

.

On xy plane it becomes much simpler. By the way, your software is great and of course you are so good in using it. Does it readily give you the projection of the object on the Cartesian planes?

 

[Gh778]

I confused, I don't understand your last message, what's dv, du ?

By the way, your software is great and of course you are so good in using it.

it's an internet drawing ;)

 

[Hassan2]

I confused, I don't understand your last message, what's dv, du ?

I used your own notation. u is the angle, so du is the differential angle which is "pas" in your code. The same for dv. So ds=v*pas*pas/cosθ .

 

[Gh778]

so for you the torque is torque=v*(uLimit-u)/10.0*(sin(a)/cos(a))*pas*pas ?

 

[Gh778]

Here the code, I have verified with circular thread (cut if in the program), it's ok, with calculator : torque = pi*2*pi*(2*pi/10)*100000=1 240 251 Nm, and with program I found 1 240 412 Nm 5 digits for accuracy. Torque=v*(uLimit-u)/10.0*(sin(a)/cos(a))*pas*pas;

With square thread:

d=0rd/s => Torque=221 544 Nm
d=-0.5rd/s => Torque=223 990 Nm

There is a difference.

I think if we make uLimit half, the torque becomes half too.

If you divided by 2 proof, you divided by 4 the torque because surface is half and pressure is half. With square thread, not exactly divided by 4 because the thread is square (depend of the start and end).

There always a torque with the square thread if the program is good, especially the torque.

The code:

#include <stdio.h>
#include <math.h>
#include <stdio.h>

int main(void)
{
double x=0.0,y=0.0,z=0.0; // each point of the circular thread, I use circular thread and after select only points which are on the square thread
double u=0.0,v=0.0; // u=altitude, v=radius
double a=0.0; // angle
double torque=0.0; // local torque
double torqueT=0.0; // total torque
double pas=0.001; // step for integration
double pi=3.1415927;
double vLimit=2.0*pi, uLimit=2.0*pi; // limit of integration, in meters
double c1=3.0, c2=4.0; // limit of the square thread in meters
double d=-0.5; // angle start for the helicoid

do
{
do
{
//calculation of each point of the helicoid
x=v*cos(u-d);
y=v*sin(u-d);
z=u;

// select only point for have the square thread
if( (x>c1 && x<c2 && y<c2 && y>-c2) || (x<-c1 && x>-c2 && y<c2 && y>-c2) || (y>c1 && y<c2 && x<c2 && x>-c2) || (y<-c1 && y>-c2 && x<c2 && x>-c2) )
{
a=atan(uLimit/2.0/pi/v);
torque=v*(uLimit-u)/10.0*(sin(a)/cos(a))*pas*pas; // Here the pressure is (uLimit-u)/10.0 in bar //// pas*pas = surface
torqueT+=torque;
/*
// print part result
printf("\nu=%f, v=%f", u,v);
printf("\nx=%f, y=%f, z=%f",x,y,z);
printf("\na=%f, couple=%f",a, torque);
printf("\nT=%f", torqueT);
system("pause");
*/
}
v+=pas; // increase step of integration
}while(v<vLimit);
v=0.0;
u+=pas; // increase step for integration
}while(u<uLimit);

printf("The total torque is: %f",torqueT*100000.0);
}

 

[Hassan2]

Right. divided by 4. I have got the same result. let me finalize my result and then share it with you.

 

[Gh778]

With step (pas) = 0.0001:

Circular thread give 1 240 254 Nm compared with 1 240 251 Nm the accuracy is on 6 digits

Square thread:

d=0 rd => Torque=221516 Nm
d=-0.5 rd => Torque=223958 Nm

I think the accuracy is big enough for see there is a torque (if the program is good).

 

[Hassan2]

First, In you code, in general, a=atan(1/v) . But for 2pi span, the result is fine.

The equation for local torque is then simplified to Torque=(uLimit-u)/10*pas*pas.

This is due to the upper surface. How about the lower surface. Also remember that the gasket is elastic. If the torque or force from one side causes deformation it, it applies a force on the surface.

 

[Gh778]

How about the lower surface.

The upper surface is for example d=0 rd and the lower surface is with d=-0.5 rd. This is what I said there is a torque (I take upper torque less lower torque).

First, In you code, in general, a=atan(1/v) . But for 2pi span, the result is fine. The equation for local torque is then simplified to Torque=(uLimit-u)/10*pas*pas.

For you the result in my program is not fine ? You suppress sin and cos ?

Also remember that the gasket is elastic. If the torque or force from one side causes deformation it, it applies a force on the surface.

For me the force on the gasket can be near zero. Except the problem of capillary action we can take the film very low as possible. And the square thread fixed the gasket on it so the deformation can be limited. It's only a technical problem.

I don't see where is another torque or another force which cancel this torque.

 

[Hassan2]

You had sin(θ)/cos(θ) which is equal to tan(θ) which is equal to 1/v . I just plugged this in your equation.

Just imagine that there is no water in the lower gap but the gasket is there. The upper force or torque deform the gasket till the thread comes to equilibrium. The force of the gasket would be as large as the hydraulic force.

 

[Gh778]

Just imagine that there is no water in the lower gap but the gasket is there. The upper force or torque deform the gasket till the thread comes to equilibrium. The force of the gasket would be as large as the hydraulic force

But there is a vertical force if we put only water at up surface. Vertical force is cancel with up and down surface only. The study is with up and down surfaces with water. The vertical force don't care about radius. If up and down surface have water, the up/down forces on gasket is 0.

The force on the gasket:

thickness of the gasket : 1µm
at bottom: 0.628 bar
on 1 meter of the gasket we have only : 1e-6*1*0.628*100000 = 0.0628 N

 

[Hassan2]

1. Even with the upper water film, you have a torque. Cancellation of the vertical force is obvious to you but how about the torque when only the upper gap is filled? You just calculated a net force due to the upper water. You need to show that this is canceled even when there is no water in the lower gap.

2. The calculation is not like that because the forces on the gaskets are not only the hydraulic forces ( these forces are negligible as you showed). The force on the thread presses it again the gasket. The thin gasket must take all the force to in the equilibrium. In case of torque cancellation,the force of the gasket must be large enough to cancel the torque of the water.

 

[Gh778]

You just calculated a net force due to the upper water.

Not at all, the upper force is give with square thread when d = 0 rd. The lower force is give with square thread when d=-0.5 rd (it's an example).

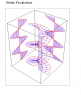
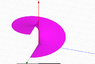
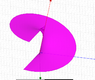
Show the 2 drawings below (circular thread for understand easily)

First drawing d=0 rd
Second drawing d= -0.5 rd
Third drawing with 2 threads

 

[Hassan2]

For d=.5 ,I get a big difference even for circular thread. In my code in my code
x=v*cos(u);
y=v*sin(u);
z=u;

I consider the d in the if branch:
if( z>d && (x>c1 && x<c2 && y<c2 && y>-c2) |...

 

[Gh778]

for d=-0.5 I don't find any difference with the circular thread: 1 240 313 with step =0.0005

Don't change on the third digit. Are you sure ?

 

[Hassan2]

OK I corrected my code. Now only for square thread I have a nonzero torque.

 

[Hassan2]

Now calculate the torque around two other axes, both passing through the center ( u= pi) one parallel with x-axis and another parallel with y axis. It must be zero for a circular thread but for a square thread I expect an nonzero one.

 

[Gh778]

Why ? if I put the square thread on an Z axis of rotation, others torque can't do anything, I think. For me the contrary torque must be on Z axis. But where ?

 

[Hassan2]

You are right they can't don anything if we have calculated them by correct forces. Because of the bearings, we don't need the other two torques because they are canceled by bearing not by the gasket.

But according to my calculation, there is a net force in -Z direction. This force must be canceled by the lowers gasket because nothing else can cancel them. The gasket forces are perpendicular to the thread surface. They can't have z component only. Their other component cause a toque around z axis. Can you calculate the total force? Then we can distribute it uniformly on the two cords of the lower gasket and recalculate the torque.