SUMMARY
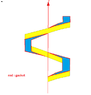
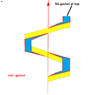
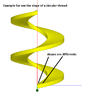
The discussion centers on calculating the torque on a square screw filled with water, specifically focusing on the interactions between external and internal surfaces and the effects of hydraulic pressure. Participants emphasize that the forces acting on differential surfaces are equal and opposite, leading to torque cancellation. The conversation highlights the importance of gasket thickness and its impact on torque calculations, particularly when considering the screw's orientation and the presence of water. Ultimately, the consensus is that understanding these forces is crucial for accurately determining the net torque on the screw.
PREREQUISITES
- Understanding of hydraulic pressure principles
- Familiarity with torque calculation methods
- Knowledge of screw thread mechanics
- Experience with differential surface analysis
NEXT STEPS
- Research "Hydraulic pressure effects on torque" for deeper insights
- Study "Differential surface force analysis" to understand force interactions
- Explore "Screw thread mechanics" to grasp various thread types and their behaviors
- Investigate "Gasket design and its impact on torque" for practical applications
USEFUL FOR
Mechanical engineers, fluid dynamics specialists, and anyone involved in the design and analysis of screw mechanisms in hydraulic systems will benefit from this discussion.