Torque Rigid Beam: Find Force Applied by Support 2

[mailmas]

Homework Statement

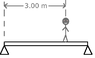
A rigid beam with a length of 4.00 m has a mass of 50.0 kg and a uniform mass distribution. It is supported at either end as seen in the figure by resting on the supports, but is not attached to them. If you call the support on the right support 2 and the support on the left support 1, a 65.0 kg person stands 3.00 m from support 1. Solve for the force applied by support 2.

Homework Equations

T=F*r

The Attempt at a Solution

Taking support 1 as pivot point:
Sum of Torques = 0 = Fnorm(4) - (50)(9.81)(2) - (65)(9.81)(3)
Fnorm(4) = (50)(9.81)(2) + (65)(9.81)(3)
Fnorm = (981 + 1912.95)/4
Fnorm = 723.5N but the answer says 405N.

 

[kuruman]

I cannot see the figure that you refer to. Can you post it?

 

[mailmas]

I cannot see the figure that you refer to. Can you post it?

Sure.

 

[kuruman]

Thanks. Your answer for the diagram you have is correct. If you solve for the force at the other end, you will get 405 N. There must be a mix up somewhere. It makes sense that the larger force is at the end closer to the person.

 

[mailmas]

Thanks. Your answer for the diagram you have is correct. If you solve for the force at the other end, you will get 405 N. There must be a mix up somewhere.

Just calculated it for the other side and got 405. Thanks for the help.