Torsional Spring Force Transfer

[ZachGriffin]

I'm trying to work out the force transfer along a torsional spring. Using Hooke's law, the opposing force from applying a force to the torsional spring can be calculated using

\textbf{F} = -\textit{K}\vartheta

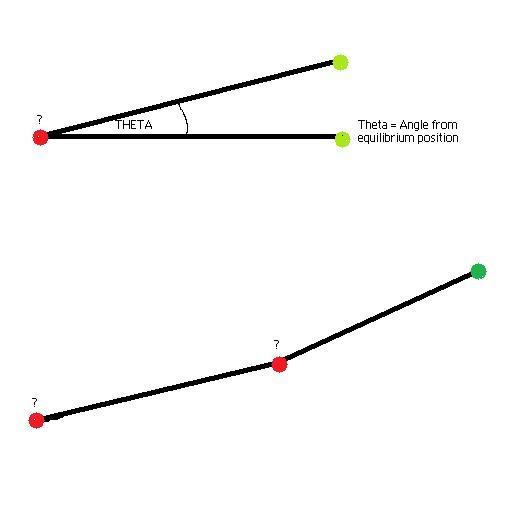
with theta representing the angular deflection from its equilibrium position and K the spring constant. Using the diagram below I can work out the forces and deflection if I applied a force at the green dots but I can't find a formula anywhere for calculating the force transferred along the beam that I would apply at the red dots. The top part of the digram represents one torsional spring, and the bottom is what I'm trying to do. I assume the formula would be something like

\textbf{F} = Force applied / \textit{K} / Distance (length of the beam)

Any help would be much appreciated

 

[tiny-tim]

Hi Zach!

Sorry, I'm not understanding the question …

transfer of force from where to where?

and a torsional spring stays where it is, and your picture seems to be showing something else.

Force should be the same all the way along a spring , just as tension is the same all the way along a ("massless") string.

 

[ZachGriffin]

Hi Tim!

Thanks for replying. What I'm trying to do is simulate the real time flexing of a group of metal tubes (chassis). For processing reasons I can't go into metallurgy algorithms so I'm treating each chassis tube member as a torsional spring. If I had 2 chassis tubes rigidly connected to each other such as in the bottom part of the diagram, and I applied an upward force at the green dot, that tube would bend like a torsion spring and apply a counter force downward depending on the spring rate and deflection. What I'm trying to work out is if those 2 tubes are connected to each other, there would be a moment created at the middle red dot. How would the spring rate effect that moment? I hope that helps you understand what I'm trying to achieve

 

[Redbelly98]

I too am trying to understand what is being asked, but I don't.

It seems that all forces and torques could be calculated without invoking spring constants, since the sums of forces and torques should be zero ... or am I missing something? Are forces being applied at each of the 3 dots? Is the deflection small compared to the length of the tubes?