Math Amateur
Gold Member
MHB
- 3,920
- 48
I am baffled by some aspects of the torus ... I hope someone can help ...
I am puzzled by some aspects of Singh's treatment of the torus in Example 2.2.5 ( Tej Bahadur Singh: Elements of Topology, CRC Press, 2013) ... ...
Singh's Example 2.2.5 reads as follows:
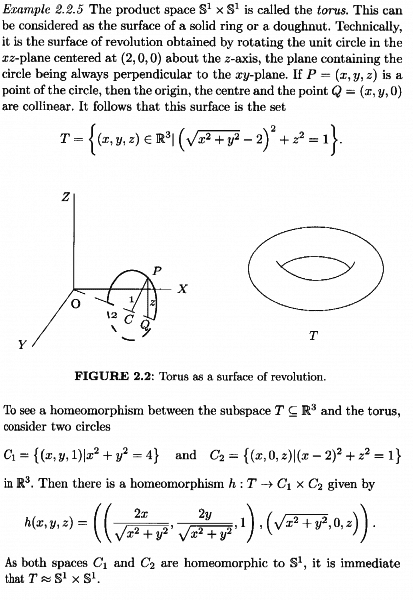
My questions related to the above example of Singh's are as follows:Question 1
C_1 as defined above seems to me to be a circle at 'height' z = 1, around the z-axis ... why (for what reason?) did Singh choose C_1 to be at 'height' z = 1?
Why not choose C_1 as \{ (x,y, 0) \ | \ x^2 + y^2 = 4 \}?
Such a choice seems more natural if you are rotating C_2 around the z-axis, since C_1 is at level z = 0 ... ...Question 2
h \ : \ T \rightarrow C_1 \times C_2
maps (x,y,z) onto two three dimensional points in Euclidean 3-space and so essentially maps (x,y,z) into Euclidean 6-space ... ..
... BUT ...
T is homeomorphic to S^1 \times S^1 which is embedded in Euclidean 4-space ... ... how can this be ...
I hope someone can clarify the above issues/questions ...
Peter
I am puzzled by some aspects of Singh's treatment of the torus in Example 2.2.5 ( Tej Bahadur Singh: Elements of Topology, CRC Press, 2013) ... ...
Singh's Example 2.2.5 reads as follows:
My questions related to the above example of Singh's are as follows:Question 1
C_1 as defined above seems to me to be a circle at 'height' z = 1, around the z-axis ... why (for what reason?) did Singh choose C_1 to be at 'height' z = 1?
Why not choose C_1 as \{ (x,y, 0) \ | \ x^2 + y^2 = 4 \}?
Such a choice seems more natural if you are rotating C_2 around the z-axis, since C_1 is at level z = 0 ... ...Question 2
h \ : \ T \rightarrow C_1 \times C_2
maps (x,y,z) onto two three dimensional points in Euclidean 3-space and so essentially maps (x,y,z) into Euclidean 6-space ... ..
... BUT ...
T is homeomorphic to S^1 \times S^1 which is embedded in Euclidean 4-space ... ... how can this be ...
I hope someone can clarify the above issues/questions ...
Peter
Attachments
Last edited:
