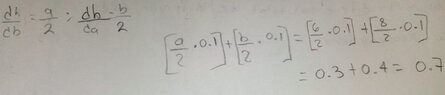- #1
Ereisorhet
- 2
- 0
I have the following problem:
Use the total differential to calculate approximately the largest error at determine the area of a triangle rectangle (right triangle) from the lengths of the cathetus if they measure 6 and 8 cm respectively, with a possible error of 0.1 cm for each measurement.
I did this:
View attachment 9034
Use the total differential to calculate approximately the largest error at determine the area of a triangle rectangle (right triangle) from the lengths of the cathetus if they measure 6 and 8 cm respectively, with a possible error of 0.1 cm for each measurement.
I did this:
View attachment 9034