Bromio
- 59
- 0
Homework Statement
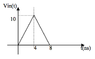
Calculate the output vo(t) if the input is the signal vin(t) shown in attached figures.
The Attempt at a Solution
I've calculated that ransfer function transmission line: H(s) = Vo(s)/Vin(s) = exp(-j*gamma*l), where gamma = -j*omega*sqrt(LC). However, tau = sqrt(LC)*l, H(j*omega) = exp(-j*tau*omega), where tau is the delay.
I know that Vo(j*omega) = H(j*omega)*Vin(j*omega). How can I continue?
Thank you.