Transformation Of Probability Density Functions

[caffeine]

Homework Statement

Let X and Y be random variables. The pdfs are f_X(x)=2(1-x) and f_Y(y) = 2(1-y). Both distributions are defined on [0,1].

Let Z = X + Y. Find the pdf for Z, f_Z(z).

Homework Equations

I'm using ideas, not equations.

The Attempt at a Solution

I'm dying of curiosity about where I'm going wrong. I'm so sure of each step, but my answer can't be correct because \int_0^2 f_Z(z)\,dz is zero! Here's my logic.

Consider the cdf (cumulative distribution function) for Z:

<br /> F_Z(z) = P(Z\le z) = P(X+Y \le z)<br />

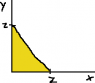
Here, F_Z(z) is the volume above the triangle shown in the image I attached to this message (in case something happens to the attachment, it's the triangle in quadrant 1 bounded by x=0, y=0 and x+y=z.)

The volume above the shaded region represents F_Z(z).

<br /> F_Z(z) = \int_{x=0}^{x=z} 2(1-x)\int_{y=0}^{y=z-x} 2(1-y)\,dy\,dx<br />

Performing the integrals gives F_Z(z) = \frac{1}{6}z^4 - \frac{4}{3}z^3 + 2z^2. Then taking the derivative of the cdf gives the pdf:

<br /> f_Z(z) = \partial_z F_Z(z) = \frac{2}{3}z^3 - 4z^2 +4z<br />

Unfortunately, this can't be right because the integral of this function over [0,2] gives zero.

I also would've expected that the maximum of f_Z(z) would be at z=0 since individually, X and Y are most likely to be zero.

I checked my algebra and calculus with Mathematica; it looked fine. I think there's a conceptual problem. There must be something I don't understand or some point I'm not clear about.

What did I do wrong?

 

[quasar987]

You have to split the problem into different cases.

i) z<0
ii) z<1
iii) 1<z<2
iv) z>2

In each case the area of integration is different. But for each case, your model for the integral is

F_Z(z)=\int\int_{\{(x,y)\in [0,1]\times[0,1]:\ y\leq z-x, \}}f_{XY}(x,y)dxdy

So you're integrating over the area that's the intersection of the square [0,1] x [0,1] with the area under the curve y=z-x.(Btw, you never said that X and Y are independant but I assume they are?)

 

[caffeine]

Ahhh... yes. I *completely* understand.

We're integrating that portion of the unit square (in QI with lower left corner at origin) that lies underneath x+y=1.

So when 0<z<1, there's only one function that represents the "top": the line x+y=z.

And when 1<z<2, there's two functions: y=1 and x+y=z, and therefore we need to break the region of integration into two portions.

Got it. Thanks.

And, yes. :-)