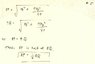songoku
- 2,470
- 383
Homework Statement
P is a point on triangle ABC such that area PAB : area PBC : area PCA = 2 : 3 : 5
a. Find AQ : QC
b. Show that BP = 0.5 BQ
Homework Equations
The Attempt at a Solution
a. i found that AQ : QC = area QAB : area QBC, but i don't know how to continue ( the answer is 2 : 3)
b. sorry, I'm clueless...
thx