AryRezvani
- 65
- 0
Tricky problem worth 2 points on my final grade :)
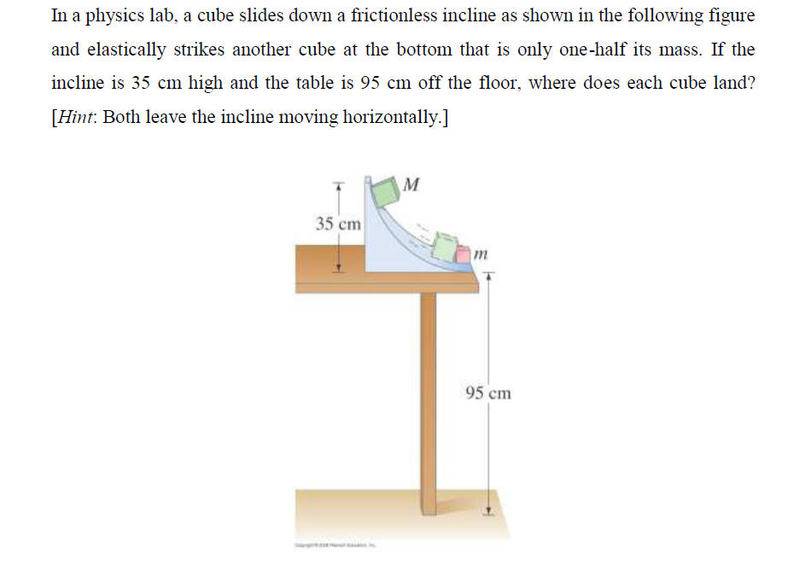
I honestly don't know how to tackle this.
I think it's going to contain ƩF=mg, and some basic kinematic equations.
Where do is start?
Homework Statement
Homework Equations
I honestly don't know how to tackle this.
I think it's going to contain ƩF=mg, and some basic kinematic equations.
The Attempt at a Solution
Where do is start?