- #1
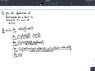
Trig idents while computing limit
Click For Summary
The discussion revolves around the difficulty in solving a limit problem using trigonometric identities. The user attempted to apply the identities for cosine and sine to expand the terms but struggled with factoring due to the presence of the sin(h) term. Another participant suggests factoring sin(x) from the first two terms and cos(x) from the next two terms to align with the solution guide. There is also confusion regarding the denominator in the user's work. The conversation highlights the importance of careful expansion and factoring in trigonometric limit problems.
First, I tried to show that ##f_n## converges uniformly on ##[0,2\pi]##, which is true since ##f_n \rightarrow 0## for ##n \rightarrow \infty## and ##\sigma_n=\mathrm{sup}\left| \frac{\sin\left(\frac{n^2}{n+\frac 15}x\right)}{n^{x^2-3x+3}} \right| \leq \frac{1}{|n^{x^2-3x+3}|} \leq \frac{1}{n^{\frac 34}}\rightarrow 0##. I can't use neither Leibnitz's test nor Abel's test. For Dirichlet's test I would need to show, that ##\sin\left(\frac{n^2}{n+\frac 15}x \right)## has partialy bounded sums...
It's easy to see that any polynomial is function of that class. Also it seems that composition of exponent and polynomial is good as well. G_f(a, b) should be equal G_f(b, a) as the f(a+b) is symmetrical.
Does anyone have information about this or at least related to it?