Trigonometric Function Application

[nolachrymose]

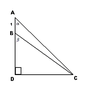
I was given the following problem to solve (diagram is attached):

In right triangle ACD with right angle at D, B is a point on side AD between A and D. The length of segment AB is 1. Is <DAC = \alpha and <DBC = \beta, then find the length of side DC in terms of \alpha and \beta.

I have tried all sorts of mixes of the trigonometric functions to solve this problem, but the closest I can get is where all the terms cancel out. Could someone possibly give me a hint as to how to start this problem, as I'm having great difficult solving it? Any help is greatly appreciated. Thank you! :)

 

[Chi Meson]

Have you tried law of sines? Think of the set up as two triangles, ABC and ADC. Try to solve first for the one side they have in common (the hypotenuse of ADC).

 

[christinono]

I was given the following problem to solve (diagram is attached):



I have tried all sorts of mixes of the trigonometric functions to solve this problem, but the closest I can get is where all the terms cancel out. Could someone possibly give me a hint as to how to start this problem, as I'm having great difficult solving it? Any help is greatly appreciated. Thank you! :)

Yeah, first represent all relevant angles in terms of alpha and beta. Then, use the sin law to solve for BC(in terms of alpha and beta). Then, use simple trig to do the rest.

 

[nolachrymose]

While I do know the Law of Sines, I'm not allowed to use it since we haven't proven it yet. However, I was able to solve it by using two simultaneous equations and substitution. My answer was this:

\frac{\tan{\beta}\tan{\alpha}}{\tan{\beta}-\tan{\alpha}}

Thank you for your suggestions, though! This always seems to happen when I post, sorry...

-----------

I have one last question before I can retire this chapter! Unfortunately, it's the hardest one I've come across so far (unless I'm missing something painfully obvious here). It asks to prove that for any point in the interior of an equilateral triangle, the sum of the lengths of the perpendiculars dropped from the point to the three sides is equal to the length of the altitude of the triangle.

I have no idea where to start on this one (which is quite rare). I've tried similar triangles, but the problem is I cannot prove that any of the lines from the interior point to the vertices are angle bisectors or anything, so I end up with triangles that have no relation to the altitude itself.

One possible approach that I could use was to use the interior point of the triangle which is the median, incenter, circumcenter, and orthocenter of the triangle (since it's equilateral), but this too I cannot do without loss of generality.

Any help is greatly appreciated! Thank you! :)