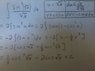Trigonometric Integrals by Substitution

[awsalazar]

I am unsure whether I have properly performed the integration of the integral ∫((sin(√x))^3*dx)/√x

When I used my TI-Nsprire CAS to take the derivative of my answer in order to check if I was correct, and it came out differently. Now I used some trig identities to manipulate the problem, so I figured that is why it was different. So when I stored the integral into one function and the solution into another function, values I would enter were different for each function. Can someone correct any errors I have made or confirm that my answer is correct?

I have attached my attempt at the integral as a .jpg file.
∫((sin(√x))^3*dx)/√x

 

[Karnage1993]

Your solution and answer are correct. Note that whatever answer your calculator had, you can merely subtract it from the original and see if the result is 0.

 

[mfb]

I don't see an error, and I can confirm that your solution is correct.

 

[awsalazar]

Thanks a lot guys, and good advice Karnage1993, a much easier process then what I was doing.