Trouble with Newton's Third Law and motion

[ecoo]

Hey guys, I have some confusion with Newton's Third Law. I understand that, for example, if I push against a wall the wall feels my force and the wall puts an equal force onto me.

One confusion comes from the horse cart problem, or any motion problem that uncludes one object pushing another.

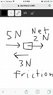
In the horse cart problem, I see how when the horse puts a force into the ground the ground puts a force onto the horse. The force acting on the horse also puts a force onto the carriage, so I can see how the cart goes forward (I look only at the forces acting on the cart). But the carriage puts a force onto the horse, which cancels out the horses' force onto the ground.

The way that i get past this I think that as the carriage goes forwards it isn't applying the equal force onto the horse, and the horse which was initially slowed down a bit then goes forward to catch up to the carriage. Once the horse "catches up", then the horse applies a force onto the carriage which pushes the horse back a tiny bit and the cycle repeats, so in a way the horse and cart are in a way bouncing off each other. Now this bouncing effect would be tiny, since the force that the carriage acts onto the horse is only acted for a tiny duration.

I'm making a mistake somewhere, could you guys explain the horse cart scenario?

Thanks!

 

[Buzz Bloom]

Hi ecoo:

Its the horse doing all the work.

The horse's harness exerts force on the cart and the cart moves. The cart's inertia pulls back against the horse's harness, and the horse feels this force as pressure on its shoulders.

The horse's hooves push backwards on the Earth which enables the horse to move forward. The friction of the Earth's surface pushes back against the hooves, which the horse's hooves feels.

The horse's weight is pulled downwards by the Earth's gravity. The surface of the Earth pushes back up equally, so the horse does not move vertically, but the horse feels the upward force on his hooves.

Hope this is helpful.

Regards,
Buzz

 

[A.T.]

the carriage puts a force onto the horse, which cancels out the horses' force onto the ground.

That doesn't make any sense: If the forces act on different bodies, they cannot cancel.

 

[ecoo]

That doesn't make any sense: If the forces act on different bodies, they cannot cancel.

My bad, I meant the force that the ground exerts onto the horse as a result of the horses' force onto the ground. The problem I don't understand is that if the force the carriage puts onto the horse is equal to the force pushing the horse, than the horse shouldn't move at all - I tried to rationalize it using the bouncing model, but I think I am missing something somewhere.

 

[Andrew Mason]

My bad, I meant the force that the ground exerts onto the horse as a result of the horses' force onto the ground. The problem I don't understand is that if the force the carriage puts onto the horse is equal to the force pushing the horse, than the horse shouldn't move at all - I tried to rationalize it using the bouncing model, but I think I am missing something somewhere.

Do a free body diagram for the horse and cart:

$F_{h-c} = F_{gravity} + F_{normal} + F_{push} - F_{friction} = m_{h-c}a_{h-c}$

If $|F_{push}| > |F_{friction}|$ then $a_{h-c}>0$

The cart always moves with the horse. So there are always balanced tensions (ie no net force) as between the cart and horse.

Once the push of the ground on the horse (due to the equal and opposite push of the horse on the ground -this is where the third law comes in) exceeds the static friction force pushing back on the cart, the horse/cart begins to accelerate. At this point the force of kinetic friction (usually a bit lower than the static force) opposes the forward motion. Once the horse and cart are moving at a desirable speed, the horse can reduce its push force to be just equal to the force of kinetic friction. At that point there is zero net force but motion continues (first law).

AM

 

[A.T.]

The problem I don't understand is that if the force the carriage puts onto the horse is equal to the force pushing the horse

Why should those forces be of equal magnitude?

 

[russ_watters]

My bad, I meant the force that the ground exerts onto the horse as a result of the horses' force onto the ground. The problem I don't understand is that if the force the carriage puts onto the horse is equal to the force pushing the horse, than the horse shouldn't move at all - I tried to rationalize it using the bouncing model, but I think I am missing something somewhere.

I think you may be stumbling a bit over the scenario and it may be beneficial for you to draw a diagram. Typically though these questions are based on the misunderstanding of Newton's 3rd law force pairs. When you push on an object and it pushes back on you with an equal and opposite force, those forces do not cancel because they act on different bodies.

 

[ecoo]

Why should those forces be of equal magnitude?

This is probably where my mistake is - I think that because whatever force the horse puts forward on the harness, then the harness puts an equal force back onto the horse.

 

[jbriggs444]

This is probably where my mistake is - I think that because whatever force the horse puts forward on the harness, then the harness puts an equal force back onto the horse.

The relevant comparison is between the force of the ground on the horse and the force of the carriage on the horse. That is what affects the motion of the horse. Those two forces are not third law partners.

 

[CWatters]

+1 to that. The friction force between the horse and ground is what accelerates both the horse and cart. The force needed to accelerate just the cart is lower.

 

[A.T.]

if the force the carriage puts onto the horse is equal to the force pushing the horse

Why should those forces be of equal magnitude?

I think that because whatever force the horse puts forward on the harness, then the harness puts an equal force back onto the horse.

That is correct. But I thought by "the force pushing the horse" you meant the force from the ground, pushing the horse forwards. There is no reason why this force should always be of equal magnitude as the force from the harness pushing the horse back. The difference of those forces accounts for the horse's acceleration.

 

[ecoo]

Hey guys, thanks for the responses but I am still struggling a bit. I have a question, and I attached a picture below. In the picture, a force pushes on the object at 5 Newtons, and the frictional force is 3 Newtons, so the net force that the object moves is 2 Newtons.

So whatever is causing a force of 5 Newtons on the object should also feel a force of 5 Newtons backwards - does this mean it has to increase its push force to keep pushing at 5 Newtons, and in the scenario we simply assume that the push force will consistly push at 5 Newtons even though in a real life scenario the pushing force would have to increase a bit to compensate? I guess my confusion stems from how whatever is causing the force can consistently apply the same force if there is an opposite reaction on that pushing force?

 

[Andrew Mason]

I am not sure if this addresses your question, but here goes:

If the horse's legs are exerting 5 N of force on the ground (horizontally), then the ground will be exerting 5 N of force on the horse. It is that force that causes the horse (and anything that is attached to it such as a cart) to accelerate forward. Of course the Earth is being pushed in the opposite direction but its acceleration is so small (due to the huge mass of the earth) that we can ignore it.

If the horse is on a light raft on a lake, the horse pushing back on the raft with a constant 5 N force would be more difficult maintain. This is because the raft accelerates backward as the horse accelerates forward and it is harder for the horse to maintain the push force.

It is actually difficult to have a constant mechanical force being applied to or by an accelerating object. You experience this with a bicycle or a car. As the bike starts to accelerate and your feet cause the pedals to increase rotational speed it becomes increasingly harder to maintain a strong force. That is where gears come in. The gears allow one to maintain a more even force as the bicycle accelerates. Horses don't have gears.

AM

 

[A.T.]

does this mean it has to increase its push force to keep pushing at 5 Newtons

If it would increase, then it wouldn't be 5 Newtons anymore, would it? But the pushing object might need other forces acting an itself, in order to accelerate together with the pushed object.

 

[ecoo]

If it would increase, then it wouldn't be 5 Newtons anymore, would it? But the pushing object might need other forces acting an itself, in order to accelerate together with the pushed object.

Sorry I'm being very thick right now, I can't seem to understand the physics.

I mean that whatever is causing the force of 5 Newtons would have to increase force to stay pushing at 5 Newtons because the object that the force is pushing has a reactionary force against the pushing force, thus making the net force of this pushing force less than 5 Newtons.

 

[A.T.]

Sorry I'm being very thick right now, I can't seem to understand the physics.

You should draw the full free body diagram with both objects, and all the forces on them.

 

[PeroK]

Sorry I'm being very thick right now, I can't seem to understand the physics.

I mean that whatever is causing the force of 5 Newtons would have to increase force to stay pushing at 5 Newtons because the object that the force is pushing has a reactionary force against the pushing force, thus making the net force of this pushing force less than 5 Newtons.

I suggest a slightly different problem. Instead of a horse and cart, let's have a motor car and a piece of string with a tin can tied to the rear bumper.

First, you drive off in the car without the tin can. Let's assume the car can move off from a standing start under the power of its engine.

Then, you tie the string with the can to the rear bumper. Now the car cannot move, because whatever force drives the car forward is canceled out by an equal and opposite force exerted by the can on the car(!?)

So, what's the solution. You ask one of your friends. He opens the boot (trunk), throws the can inside and asks you to try again. This time, the car sets off again quite happily with the can safely in the boot, rather than pulling the car back.

Then, someone else notices your car is a Ford. She takes the can out of the boot, draws the Ford logo on it and says: "okay, now the string and the can are part of the car". It's just another component of the bumper. What happens then? If the can is part of the car, can the car move again?

 

[russ_watters]

I mean that whatever is causing the force of 5 Newtons would have to increase force to stay pushing at 5 Newtons because the object that the force is pushing has a reactionary force against the pushing force, thus making the net force of this pushing force less than 5 Newtons.

Increase from what? The situation you are showing is not changing (except that it is accelerating). The 5 Newton force is 5 Newtons. Period.

 

[Andrew Mason]

Sorry I'm being very thick right now, I can't seem to understand the physics.

I mean that whatever is causing the force of 5 Newtons would have to increase force to stay pushing at 5 Newtons because the object that the force is pushing has a reactionary force against the pushing force, thus making the net force of this pushing force less than 5 Newtons.

If a force of 5 N is applied by body A to body B then body B applies a force of -5 N to body A (ie. equal magnitude in the opposite direction). The net force on B is 5 N. The net force on A is -5N .

The total force on A + B together is 0, which means that the state of motion of the centre of mass of the two masses A+B does not change (the first law). So we can see that the third law follows from the first law.

AM

 

[CWatters]

So whatever is causing a force of 5 Newtons on the object should also feel a force of 5 Newtons backwards - does this mean it has to increase its push force to keep pushing at 5 Newtons,

No, it doesn't have to increase the FORCE but it does have to deliver more POWER...

The force is constant at 5 Newtons but the object is accelerating so the velocity is increasing and

Power = force * velocity

so whatever is causing the 5 Newton force has to produce more and more power as the object accelerates.

 

[ecoo]

I've been thinking about it, and I think that I may have finally reached somewhat of an understanding.

When thinking of the force the ground exerts on the horse (as a result of the horse pushing the ground), we look at this force accelerating the horse and cart as a whole. So if the ground pushes the horse at 10N, we look at this 10N pushing the whole mass of the cart and horse. The rope forces is just the tension between the horse and cart that accounts the increase in cart's acceleration and decrease in the horse's acceleration (relative to if the 10N force were just acting on the horse or cart themselves).

If the above correct? Thanks so much, you guys helped me tremendously.

 

[Andrew Mason]

I've been thinking about it, and I think that I may have finally reached somewhat of an understanding.

When thinking of the force the ground exerts on the horse (as a result of the horse pushing the ground), we look at this force accelerating the horse and cart as a whole. So if the ground pushes the horse at 10N, we look at this 10N pushing the whole mass of the cart and horse. The rope forces is just the tension between the horse and cart that accounts the increase in cart's acceleration and decrease in the horse's acceleration (relative to if the 10N force were just acting on the horse or cart themselves).

If the above correct? Thanks so much, you guys helped me tremendously.

Just about. The phrase "accounts for the increase in the cart's acceleration" is not quite right. The rope force between the horse and cart (less the force on the cart due to rolling friction) accounts for the cart's acceleration.

 

[PeroK]

I've been thinking about it, and I think that I may have finally reached somewhat of an understanding.

When thinking of the force the ground exerts on the horse (as a result of the horse pushing the ground), we look at this force accelerating the horse and cart as a whole. So if the ground pushes the horse at 10N, we look at this 10N pushing the whole mass of the cart and horse. The rope forces is just the tension between the horse and cart that accounts the increase in cart's acceleration and decrease in the horse's acceleration (relative to if the 10N force were just acting on the horse or cart themselves).

If the above correct? Thanks so much, you guys helped me tremendously.

I think you spent too long thinking about the same situation. The key to resolving these problems in your mind is to adjust the situation so that the problem becomes absurd. You used a horse and cart and imagined the cart to be as large and heavy as the horse. This caused you to believe that all forces could be equal. If, instead, you had considered the horse pulling something very light: a tin can tied to its tail, for example, you would see that a tin can can't resist horse power and the tension in the string would be negligible compared to the force the horse is exerting on the ground.

Although you've essentially solved the problem, you still seem reluctant to accept that two forces can be of different magnitudes. Newton's law doesn't say that all forces in the universe are of equal magnitude. Nor that all forces for a given system are of equal magnitude. Forces come in equal pairs, that's all.

I would sum up the solution as follows:

$F$ is the force exerted by the horse on the ground
$F$ is the force exerted by the ground on the horse (Newton's third law)

$f$ is the force exerted by the horse on the cart through tension in the rope
$f$ is the force exerted by the cart on the horse (Newton's third law again)

There is nothing to suggest that $F = f$ as you have assumed throughout.

Total force on cart: $f$
Total force on horse: $F - f$
Total force on ground $-F$

So, you'll see that the forces on the Earth-horse-cart system are balanced, but each component has an unbalanced force acting on it. Hence, all three move. Although the movement of the Earth will, of course, be negligible.

 

[ecoo]

I think you spent too long thinking about the same situation. The key to resolving these problems in your mind is to adjust the situation so that the problem becomes absurd. You used a horse and cart and imagined the cart to be as large and heavy as the horse. This caused you to believe that all forces could be equal. If, instead, you had considered the horse pulling something very light: a tin can tied to its tail, for example, you would see that a tin can can't resist horse power and the tension in the string would be negligible compared to the force the horse is exerting on the ground.

Although you've essentially solved the problem, you still seem reluctant to accept that two forces can be of different magnitudes. Newton's law doesn't say that all forces in the universe are of equal magnitude. Nor that all forces for a given system are of equal magnitude. Forces come in equal pairs, that's all.

I would sum up the solution as follows:

$F$ is the force exerted by the horse on the ground
$F$ is the force exerted by the ground on the horse (Newton's third law)

$f$ is the force exerted by the horse on the cart through tension in the rope
$f$ is the force exerted by the cart on the horse (Newton's third law again)

There is nothing to suggest that $F = f$ as you have assumed throughout.

Total force on cart: $f$
Total force on horse: $F - f$
Total force on ground $-F$

So, you'll see that the forces on the Earth-horse-cart system are balanced, but each component has an unbalanced force acting on it. Hence, all three move. Although the movement of the Earth will, of course, be negligible.

Hey, thanks for the reply. You pretty much summed up my thoughts. Quick question, I've heard that if you look at the system of the horse and cart the momentum is still conserved - or something along those lines. Could you explain this concept to me?

And what did you mean by "you'll see that the forces on the horse-cart system are balanced"?

 

[PeroK]

Hey, thanks for the reply. You pretty much summed up my thoughts. Quick question, I've heard that if you look at the system of the horse and cart the momentum is still conserved - or something along those lines. Could you explain this concept to me?

And what did you mean by "you'll see that the forces on the horse-cart system are balanced"?

If you consider the horse and cart as your system, then that system is not "closed". There is an outside element, which is the Earth. The horse is using the Earth to push against. Therefore, momentum is not conserved in the horse-cart system. They start with 0 momentum but manage to generate momentum. The forces on this system are not balanced.

If, however, you consider the horse, cart and Earth as your system, then that system is closed. And, momentum is conserved. The momentum gained by the horse and cart is offset by an equal and opposite change in momentum of the Earth. In this case the forces must be balanced.

 

[ecoo]

If you consider the horse and cart as your system, then that system is not "closed". There is an outside element, which is the Earth. The horse is using the Earth to push against. Therefore, momentum is not conserved in the horse-cart system. They start with 0 momentum but manage to generate momentum. The forces on this system are not balanced.

If, however, you consider the horse, cart and Earth as your system, then that system is closed. And, momentum is conserved. The momentum gained by the horse and cart is offset by an equal and opposite change in momentum of the Earth. In this case the forces must be balanced.

Thanks man. Another question, does this mean that if the horse can't pull the cart then F = f?

 

[PeroK]

Thanks man. Another question, does this mean that if the horse can't pull the cart then F = f?

Yes. Let's say the cart is a heavy load, not on wheels, on rough ground, so that there is a large frictional force to overcome to move it. If $F$ is the largest force that the horse can generate and it can't move the load, then $f = F$. But, now there is another force: the frictional force will also be $F$. Andyou have the situation:

The Earth is pushing the horse forward and the load is pulling the horse back equally.

The horse is pulling the load forward but the Earth (through friction) is pulling the load back.

The horse is pushing the Earth backwards, but the load (through friction) is pulling the Earth forward.

So, all three bodies have a balanced set of forces and nothing moves. This is called static equilibrium.

 

[ecoo]

Yes. Let's say the cart is a heavy load, not on wheels, on rough ground, so that there is a large frictional force to overcome to move it. If $F$ is the largest force that the horse can generate and it can't move the load, then $f = F$. But, now there is another force: the frictional force will also be $F$. Andyou have the situation:

The Earth is pushing the horse forward and the load is pulling the horse back equally.

The horse is pulling the load forward but the Earth (through friction) is pulling the load back.

The horse is pushing the Earth backwards, but the load (through friction) is pulling the Earth forward.

So, all three bodies have a balanced set of forces and nothing moves. This is called static equilibrium.

THANK YOU so much friend!