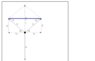
Twin spring system with a mass in between (X and Y direction)

[BvU]

Your simulation is not interested in equilibrium, so just define that position as your origin. Do as @haruspex advises and write out $\vec F = m\vec a$ equations in x and y

 

[haruspex]

Height = √(L_spring²-30²)
M_g = m*g
k = (m*g)-(L_stretched-L_rest)

Vertical force balance equation: F_g = F₁₊₂ Sum of forces in Y direction is 0 @ equilibrium(not sure if this is what you mean)

A few errors there.
I defined L as the unstretched length, so use that, no numbers!
So the stretched length is √(L²+h²)
So how much is the extension? What is the tension? What is the vertical component of the tension?

 

[MrNewton]

So how much is the extension? What is the tension? What is the vertical component of the tension?

But h is unknown? In know h of 1 spring in vertical component is 9,81 m/s² because total vertical component is 19,62 but i cannot use this to calculate the length of the stretched spring can i? Since thet have different units

 

[haruspex]

But h is unknown?

That's why we write equations containing unknowns, so that we can find out what they are. Just follow the steps in post #32. Don't worry for now about which are known and which unknown.

 

[MrNewton]

That's why we write equations containing unknowns, so that we can find out what they are. Just follow the steps in post #32. Don't worry for now about which are known and which unknown.

Alright:

Extension = Stretched length - Length @ rest
Tension = -k * Extention
Vertical component of tension = SIN(theta)*Tension OR √(Heigth²+length@rest²)

With Theta i mean the angle between the spring and the ceiling.

 

[haruspex]

Alright:

Extension = Stretched length - Length @ rest
Tension = -k * Extention
Vertical component of tension = SIN(theta)*Tension OR √(Heigth²+length@rest²)

With Theta i mean the angle between the spring and the ceiling.

Nearly right. You missed a term in the expression for sin(θ) after OR, and there's another equation relating stretched length to other lengths.
But using software-style names for the variables is going to be painful. Can we agree on L for relaxed length, s for extension, T for tension, h for height?

 

[MrNewton]

So here are my equations for this diagram:

F_g = m*g
T₁ = √(F_1y²+F_1x²)
T₂ = √(F_2y²+F_2x²)
Height from mass to ceiling = Sin(theta)*T2
T_1x = √(T_1²-T_1y²)
T_1y = √(T_1²-T_1x²)

STILL TYPING...

 

[MrNewton]

Nearly right. You missed a term in the expression for sin(θ) after OR, and there's another equation relating stretched length to other lengths.
But using software-style names for the variables is going to be painful. Can we agree on L for relaxed length, s for extension, T for tension, h for height?

Deal. I was trying to avoid miscommunication, but i agree.

Do i need to write down every equation possible for h? I know there are multiple ways to calculate, but i figured i only need 1 of them

 

[haruspex]

So here are my equations for this diagram:

F_g = m*g
T₁ = √(F_1y²+F_1x²)
T₂ = √(F_2y²+F_2x²)
Height from mass to ceiling = Sin(theta)*T2
T_1x = √(T_1SUP]2[/SUP]-T_1y²)
T_1y = √(T_1SUP]2[/SUP]-T_1x²)

STILL TYPING...

Seems to be some confusion between forces and distances.

 

[MrNewton]

Seems to be some confusion between forces and distances.

Well, i have tried for over a full day now, and i have to say with your help i came a lot further, but i keep guessing and writing on this forum with the hope that i write down what you ask me. But because of that this topic has become very messy (in my opinion). Perhaps you can tell me what you mean? Dont get me wrong here, i understand that you want me to figure it out myself (and i will!), so i will never forget it. Its a homework forum after all (and i 100% agree, but there comes a time that i really would like someone to answer this piece of the question for me, just like a teacher does after a certain amount of trying)

Im not sure what i should type anymore because i feel like i have typed everything i needed to type, but i never seem to hit the right answer.
I know the equations and pythagoras etc, i just don't know very well how to apply them into this setting because of the units. So perhaps you (or someone else reading this) can show me what you mean. Which equations are you referring to?

And offcourse teaching someone something via the internet is a lot harder then in real life. I understand that

 

[BvU]

Check your equations -- first 3 are ok, number 4 has a length on the left and a force on the right
last 2 have typos and I suspect one sign error

And: take a rest, count to 10, breathe in, out, in.. etc. etc.

You're doing fine and are getting pretty darn close too

 

[BvU]

Some - perhaps useful - comments:
You have T and F but: what's the difference ?
What happened to $|\vec T_i | = k (L_i - L_{i, 0})\$ ?
You use one $\theta$, but as soon as the mass is off zero on the x-axis, there will be two different ones

remember: you are going to integrate the equations of motion $\vec F = m\vec a$ so you will need a $\vec F(x, y)$ .

 

[MrNewton]

Check your equations -- first 3 are ok, number 4 has a length on the left and a force on the right
last 2 have typos and I suspect one sign error

And: take a rest, count to 10, breathe in, out, in.. etc. etc.

You're doing fine and are getting pretty darn close too

Thanks! I needed those words

You are referring to my post #37 with this comment?
Height from mass to ceiling = Sin(theta)*T2
This formula. Well this is exactly a problem I am dealing with. How do i calculate this? Since i want to know a distance, but i only know a force and an angle. I should calculate the length of the spring with Hooke's law? And if i know the distance of the spring i can calculate the height?By typos you mean the [SU.B] ? They have been fixed

You

 

[BvU]

You are referring to my post #37 with this comment? $\qquad$ yes
Height from mass to ceiling = Sin(theta)*T2 $\qquad$ No. $L_2 \sin\theta_2$ (which happens to be equal to $L_1 \sin\theta_1$ -- so there you have an equation too ! )
They have been fixed $\qquad$ Good. Still think you'd better keep to either F or T, not both.

If at equilibrium the mass is at position (0,0), can you develop a function $\vec F (x,y)$ ?

 

[MrNewton]

Height from mass to ceiling = Sin(theta)*T2 \qquad No. L2sinθ2L2sin⁡θ2L_2 \sin\theta_2 (which happens to be equal to L1sinθ1L1sin⁡θ1L_1 \sin\theta_1 -- so there you have an equation too ! )

Or i can use tan(theta) = h/l
h = tan(theta)*l (they are both lengths)?

//(l = relaxed spring)

$\vec F(x, y)$ ?

Not sure what the ## means?

 

[haruspex]

Not sure what the ## means?

LaTeX introducer. Didn't work for some reason. Should read $\vec F(x, y)$

 

[BvU]

Bedime for me (for Newton too!)

 

[MrNewton]

.

If at equilibrium the mass is at position (0,0), can you develop a function $\vec F (x,y)$ ?

I think i can. Does this mean i got the equations right? Should i inplement the sharp force from the left already? By that i mean make F1_x 100 Newton for example?

 

[BvU]

I think i can. Does this mean i got the equations right?

Not yet. re-read the various comments
Make things explicit: parameters (like $L_0$) , variables like $L_1, L_2, \theta_1, \theta_2$ that you want to express in relationships with $x$ and $y$ until you have as many equations as you have unknowns -- otherwise the problem is unsolvable (and yours is not unsolvable)

Should i inplement the sharp force from the left already? By that i mean make F1_x 100 Newton for example?

Certainly not ! There is no information re Force, except 'krachtstoot', i.e. impulse. I hate to give away too much, so all I can say is: modelling a force from the left is not in order. All you are given is the input of a small whack for which you may assume some value (and will need to for a numerical simulation). For now, all you need is a symbol. Think 'what does this mean for the simulation ?'.

 

[MrNewton]

Not yet. re-read the various comments
Make things explicit: parameters (like $L_0$) , variables like $L_1, L_2, \theta_1, \theta_2$ that you want to express in relationships with $x$ and $y$ until you have as many equations as you have unknowns -- otherwise the problem is unsolvable (and yours is not unsolvable)'.

Alright, i have written al the possible equations for θ₁, θ₂, L₁, L₂.

θ₁:
SIN(h/L₁)θ₂:
SIN(h/L₂)h:
SIN(θ₁) * L₁
SIN(θ₂) * L₂

L1:
h/SIN(θ₁)

L2:
h/SIN(θ₂)

 

[BvU]

If the mass moves 1 unit of length in the +x direction, what is the change in $L_1$ ? And in $L_2$ ? This has consequences for $F_1, F_{1,x}, F_{1,y}, \theta_1, F_2, F_{2,x}, F_{2,y}, F_{tot, x}, F_{tot, y}, \theta_2$ so also for $a_x, a_y$

[edit] and $\sin\theta_1 = h/L_1 \quad \Rightarrow \quad \theta_1 = \arcsin (h/L_1)$, etc !

 

[BvU]

The simulation you are setting up will integrate the equations of motion, $\vec {\bf a} = \vec {\bf F} / m$

At $t_0 = 0$ you have $$ x_0 = 0, \\ y_0= 0, \\ v_{x,0} = ..., \\ v_{y,0} = ... , \\ a_{x,0} = 0, \\ a_{y,0} = 0
$$With the simplest integrator, forward Euler, you can calculate the situation
at t = $t_0 + \Delta t$:$$ x = x_0 + v_{x_0} \Delta t , \\ y = y_0 + v_{y,0} \Delta t, \\ v_{x} = v_{x_0} + a_{x,0} \Delta t \\
v_{y} = v_{y_0} + a_{y,0} \Delta t
$$ and then you need to calculate a new $\vec {\bf a}$ at position $\left (x(\Delta_t), y(\Delta_t) \right )$
and so on.

 

[MrNewton]

The simulation you are setting up will integrate the equations of motion, $\vec {\bf a} = \vec {\bf F} / m$

For some reason i cannot reply your equation without the site going nuts.

(

Thanks for those equations. THIS ONE, : X = X₀ + V₀ * ΔT, Shouldtn it be, X_n = X_n-1 + V_n * ΔT ?
With n the current timestep
So the current speed instead of the previous speed?

and for the acceleration:, a_n+1 = F_n+1/m

 

[haruspex]

Thanks for those equations. THIS ONE, : X = X₀ + V₀ * ΔT, Shouldtn it be, X_n = X_n-1 + V_n * ΔT ?
With n the current timestep
So the current speed instead of the previous speed?

and for the acceleration:, a_n+1 = F_n+1/m

The starting point is the position and velocity, $\vec r_0$, $\dot{\vec r}_0$.
From these you calculate an acceleration, $\ddot {\vec r}_0$.
For the next timestep, $\dot {\vec r}_1=\dot{\vec r}_0+\ddot {\vec r}_0\Delta t$.
So for calculating $\vec r_1$ you have two velocities available. Taking the average should work well.