Two disks -- An educational problem

[wrobel]

Let me share an educational problem which I learned from my friend Prof. M. Kirsanov. Perhaps somebody finds it interesting to discuss it with students. I do.
The problem is pure kinematic.

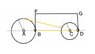
Assume we have two disks which can rotate about their fixed centers $A,C,\quad |AC|=b$. The radii of the disks are $R,r,\quad R>r$ respectively. The discks are connected by a rigid bridge $BFGD$ and $B,D$ are the hinges placed on the rims of the disks. At one moment the system has the position that is shown at the picture ; the angular velocity and the angular acceleration of the left disk are given: $\omega,\varepsilon$.
Find angular velocity and angular acceleration of the right disk at this moment.

Can the system move in the vicinity of shown position? What is configuration space of this system? What if $r=R$?

 

[anuttarasammyak]

Is connected by rigid bridge BFGD is same with connected by rigid rod BD in considering the motion ?

 

[wrobel]

yes

 

[A.T.]

What if $r=R$?

Then it's like linked locomotive wheels going at the same rate.

 

[etotheipi]

Ooo okay, I try the first part, but I maybe screw it up. Since$$\left(\frac{d}{dt}\right)_{t=t_0} \mathbf{BD} = (\omega_2 r - \omega R) \mathbf{e}_y$$and$$\left( \frac{d^2}{dt^2}\right)_{t=t_0} \mathbf{BD} = (\varepsilon_2 r - \varepsilon R) \mathbf{e}_y - (\omega_2^2 r - \omega^2 R) \mathbf{e}_x$$Point D constrained to perform circular motion about point B, i.e. $\frac{d}{dt}|\mathbf{BD}| = 0$, so we have$$ (\omega_2^2 r - \omega^2 R) = (b+r-R)\left( \frac{\omega_2 r - \omega R}{b+r-R} \right)^2$$or in other words that$$\omega_2^2 r(b-R) + 2 \omega r R \omega_2 - \omega^2 R(b+r) = 0$$so in that case

$$\begin{align*}

\omega_{2,\pm} = \frac{-2 \omega r R \pm \sqrt{4 \omega^2 r^2 R^2 + 4R r \omega^2 (b-R)(b+r)}}{2r(b-R)} &= \left[ \frac{-r R \pm \sqrt{Rrb \rho}}{r(b-R)} \right] \omega

\end{align*}$$where $\rho = |BD| = b + r - R$.

 

[wrobel]

I have written formulas just for the case
ω≠0, ρ=b+r−R>0, $R>r$
my result is
$$\omega_*=\omega p_\pm,\quad \varepsilon_*=\varepsilon p_\pm,\quad p_\pm=\frac{Rr\pm\sqrt{R\rho br}}{r(R-r)}$$

 

[anuttarasammyak]

Let us take xy coordinate for moving points
$$B=(R\cos\theta,R\sin\theta)$$
$$D=(b+r \cos\phi, r \sin\phi)$$
BD^2 is constant
$$(b-R+r)^2=(R\cos\theta-b-r \cos\phi)^2+(R\sin\theta-r \sin\phi)^2$$
$$bR(1-\cos\theta)-br(1-\cos\phi)+Rr(1-\cos(\theta-\phi))=0...(1)$$
Taking time derivative
$$bR\sin\theta\dot{\theta}-br\sin\phi\dot{\phi}+Rr\sin(\theta-\phi)(\dot{\theta}-\dot{\phi})=0...(2)$$
Taking time derivative again
$$bR\sin\theta\ddot{\theta}-br\sin\phi\ddot{\phi}+Rr\sin(\theta-\phi)(\ddot{\theta}-\ddot{\phi}) +bR\cos\theta\dot{\theta}^2-br\cos\phi\dot{\phi}^2+Rr\cos(\theta-\phi)(\dot{\theta}-\dot{\phi})^2=0...(3)$$
These three equations show constraints on angle, angular velocity and angular acceleration.

For $\theta=\phi=0$ , (3) becomes
$$bR\dot{\theta}^2-br\dot{\phi}^2+Rr(\dot{\theta}-\dot{\phi})^2=0$$
quadratic equation of $\dot{\phi}$ with $\dot{\theta}$ given. The solution is
$$\dot{\phi}=\dot{\theta}[ \frac{\pm\sqrt{\frac{b\rho}{Rr}}-1}{\frac{b}{R}-1}]$$
where
$$\rho=b-R+r$$
As $\frac{b\rho}{Rr}>1$, + solution: ortho, - solution: reverse rotation.

Ref. post #4 in the special case of $R=r$,$\rho=b$ and
+ solution
$$\dot{\phi}_+=\dot{\theta}$$
like locomotive wheels.
- solution
$$\dot{\phi}_-=-\dot{\theta}\frac{\frac{b}{R}+1}{\frac{b}{R}-1}$$EDIT as suggested by @wrobel in post #8, time derivative of (3) after making $\theta=\phi=0$ is
$$bR\dot{\theta}\ddot{\theta}-br\dot{\phi}\ddot{\phi}+Rr(\dot{\theta}-\dot{\phi})(\ddot{\theta}-\ddot{\phi})=0$$
It would give the solution $\ddot{\phi}_{\pm}$ with $\dot{\theta}, \ddot{\theta}, \dot{\phi}_{\pm}$ provided,

$$\frac{\ddot{\phi}}{\ddot{\theta}}=\frac{1}{1+\frac{b}{R}} (-1+\frac{\frac{\frac{b}{r}\frac{b}{R}+\frac{b}{r}+\frac{b}{R}}{1+\frac{b}{R}}}{\frac{\dot{\phi}}{\dot{\theta}}-\frac{1}{1+\frac{b}{R}}}).$$

Using the previous result,
$$\frac{\ddot{\phi}_\pm}{\ddot{\theta}}=\frac{1}{1+\frac{b}{R}} (-1+\frac{\frac{\frac{b}{r}\frac{b}{R}+\frac{b}{r}+\frac{b}{R}}{1+\frac{b}{R}}}{[ \frac{\pm\sqrt{\frac{b\rho}{Rr}}-1}{\frac{b}{R}-1}]-\frac{1}{1+\frac{b}{R}}}).$$

 

[wrobel]

et us take xy coordinate for moving points

my argument was the same but

These three equations

there are no three equations: for $\theta=\phi=0$ (2) vanishes and we have to calculate $\frac{d^3}{dt^3}$

Then it's like linked locomotive wheels going at the same rate.

for $R>r$ there are two solutions. I am not sure that for $R=r$ the solution is unique

the function $f(\phi,\theta)=|BD|^2$ has a saddle point at $\phi=\theta=0$.
The equation $f=\rho^2$ gives two intersecting curves in the plane $(\phi,\theta)$.
That is the point:)

 

[A.T.]

I am not sure that for $R=r$ the solution is unique

It's not. The wheels can go in the same or opposite directions. But I think they will have the same speed in both cases.

 

[wrobel]

in my formulas the expression $(R-r)$ must be replaced with $(R-b)$
Pardon

 

[etotheipi]

I realized that in my initial expression I let $b = |BD|$, whilst it is actually defined $b = |AC|$. So I corrected that now in my post #5, and get the same as wrobel

 

[anuttarasammyak]

Using notation of my post #7 the range of angles are
$\theta[-\theta_0,+\theta_0]$ for R $\geq$ r
which satisfy law of sines
$$\frac{\sin\theta_0}{\rho+r}=\frac{\sin(\pi-\phi_0)}{R}=\frac{\sin(\phi_0-\theta_0)}{b}$$
where
$$\rho=b-R+r$$

Figure attached. Thanks @wrobel.

 

[Dr.D]

Isn't this simply the classic four bar linkage routinely studied in Theory of Machines?

 

[A.T.]

Consider the wheels almost touching. If the RH wheel rotates anticlockwise though some angle, moving D to D', then a circle radius BD centred on D' will intersect the LH wheel rim in two places, but both will be above the line BD.

I see one intersection above and one below. But they have different distances to BD, so for opposite rotation the speeds are not the same all the time. For same rotation direction the speeds are the same.

 

[haruspex]

I see one intersection above and one below. But they have different distances to BD, so for opposite rotation the speeds are not the same all the time. For same rotation direction the speeds are the same.

You are right, my mistake.

 

[Lnewqban]

 

[BvU]

Dazzling. But how about

rigid bridge BFGD

 

[A.T.]

Dazzling. But how about

rigid bridge BFGD

The BFGD bridge is not shown in the aninmation by @Lnewqban, but it is rigid. All you need is BD to have constant length.

 

[BvU]

Oops, of course. Total goof !