Two equations of generalized forces

[Kashmir]

Wikipedia article under generalized forces says

Also we know that the generalized forces are defined as

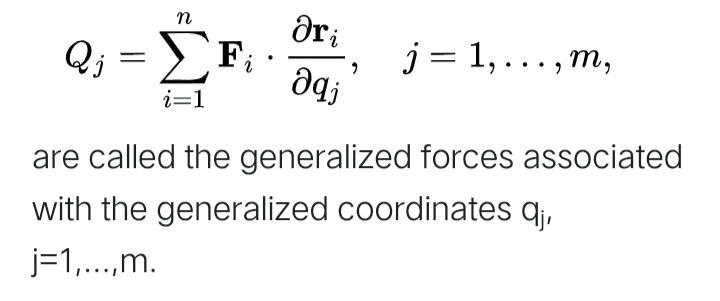How can I derive the first equation from the second for a monogenic system ?

 

[dextercioby]

What is the definition of F_i in the second equation?

 

[Kashmir]

What is the definition of F_i in the second equation?

$F_i$ is the force on the ith particle

 

[ergospherical]

You have it the wrong way around! There are some mechanical systems for which $Q_j$ can be written in the form $Q_j = \dfrac{d}{dt} \dfrac{\partial U}{\partial \dot{q}^j} - \dfrac{\partial U}{\partial q^j}$, where $U$ is called a velocity dependent potential.

[for example, the Lorentz force is derivable from the velocity dependent potential $U = q\phi - q \dot{\mathbf{r}}\cdot \mathbf{A}$]

If this is the case, then it follows that Lagrange's equation $\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{q}^j} - \dfrac{\partial T}{\partial q^j} = Q_j$ can be written in Lagrangian form by taking $L(q,\dot{q},t) = T(q,\dot{q},t) - U(q,\dot{q},t)$.

 

[Kashmir]

You have it the wrong way around! There are some mechanical systems for which $Q_j$ can be written in the form $Q_j = \dfrac{d}{dt} \dfrac{\partial U}{\partial \dot{q}^j} - \dfrac{\partial U}{\partial q^j}$, where $U$ is called a velocity dependent potential.

[for example, the Lorentz force is derivable from the velocity dependent potential $U = q\phi - q \dot{\mathbf{r}}\cdot \mathbf{A}$]

If this is the case, then it follows that Lagrange's equation $\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{q}^j} - \dfrac{\partial T}{\partial q^j} = Q_j$ can be written in Lagrangian form by taking $L(q,\dot{q},t) = T(q,\dot{q},t) - U(q,\dot{q},t)$.

You have it the wrong way around! There are some mechanical systems for which $Q_j$ can be written in the form $Q_j = \dfrac{d}{dt} \dfrac{\partial U}{\partial \dot{q}^j} - \dfrac{\partial U}{\partial q^j}$, where $U$ is called a velocity dependent potential.

[for example, the Lorentz force is derivable from the velocity dependent potential $U = q\phi - q \dot{\mathbf{r}}\cdot \mathbf{A}$]

If this is the case, then it follows that Lagrange's equation $\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{q}^j} - \dfrac{\partial T}{\partial q^j} = Q_j$ can be written in Lagrangian form by taking $L(q,\dot{q},t) = T(q,\dot{q},t) - U(q,\dot{q},t)$.

Thank you for your reply but Why have I it the wrong way around ?
You also seem to say the same thing which I'm saying.

In all cases isn't the generalized force $Q_{j}=\sum_{i=1}^{n} \mathbf{F}_{i} \cdot \frac{\partial \mathbf{r}_{i}}{\partial q_{j}}$ and for some situations (monogenic) it reduces to $\mathcal{F}_{i}=-\frac{\partial \mathcal{V}}{\partial q_{i}}+\frac{d}{d t}\left(\frac{\partial \mathcal{V}}{\partial \dot{q}_{i}}\right)$ which I can't prove how.
Please tell me what I'm doing wrong. I don't have a teacher.
God bless you

 

[ergospherical]

that’s correct. in some (special) cases the generalised force takes that second form. there’s nothing to prove!

 

[Kashmir]

that’s correct. in some (special) cases the generalised force takes that second form. there’s nothing to prove!

Maybe I'm not clear.
Do you agree that we have defined generalized forces In all cases as $Q_{j}=\sum_{i=1}^{n} \mathbf{F}_{i} \cdot \frac{\partial \mathbf{r}_{i}}{\partial q_{j}}$ .

If that's true then the definition of generalized forces for monogenic systems is the same.
But it's said that the generalized force in the monogenic system is different given as $\mathcal{F}_{i}=-\frac{\partial \mathcal{V}}{\partial q_{i}}+\frac{d}{d t}\left(\frac{\partial \mathcal{V}}{\partial \dot{q}_{i}}\right)$.

So there is a contradiction. And the only way to resolve it is to prove that they are equivalent for the monogenic case,which I cant.

I hope I'm clear. Thank you again :)

 

[Kashmir]

that’s correct. in some (special) cases the generalised force takes that second form. there’s nothing to prove!

What are those special cases? Under those special cases we should be able to move from $Q_{j}=\sum_{i=1}^{n} \mathbf{F}_{i} \cdot \frac{\partial \mathbf{r}_{i}}{\partial q_{j}}$ to $\mathcal{F}_{i}=-\frac{\partial \mathcal{V}}{\partial q_{i}}+\frac{d}{d t}\left(\frac{\partial \mathcal{V}}{\partial \dot{q}_{i}}\right)$

 

[ergospherical]

e.g. the Lorentz force
for example take the generalised coordinates to be the cartesian coordinates $\mathbf{r} = (x,y,z)$
and let $U(\mathbf{r}, \dot{\mathbf{r}}) = q\phi(\mathbf{r}) - q\dot{\mathbf{r}} \cdot \mathbf{A}(\mathbf{r})$ be a velocity dependent potential

then $\dfrac{\partial U}{\partial x_j} = q\dfrac{\partial \phi}{\partial x_j} - q\dot{x}_i \dfrac{\partial A_i}{\partial x_j}$
and $\dfrac{d}{dt} \dfrac{\partial U}{\partial \dot{x}_j} = -q \dfrac{dA_j}{dt}$
therefore\begin{align*}
Q_j = \dfrac{d}{dt} \dfrac{\partial U}{\partial \dot{x}_j} - \dfrac{\partial U}{\partial x_j} &= -q \dfrac{dA_j}{dt} - q\dfrac{\partial \phi}{\partial x_j} + q\dot{x}_i \dfrac{\partial A_i}{\partial x_j} \\

&= q \dot{x}_i \left( \dfrac{\partial A_i}{\partial x_j} - \dfrac{\partial A_j}{\partial x_i}\right) - q\dfrac{\partial \phi}{\partial x_j}
\end{align*}the first term can be rewritten as\begin{align*}
[\dot{\mathbf{r}} \times (\nabla \times \mathbf{A})]_j &= \epsilon_{jkl} \dot{x}_k (\nabla \times \mathbf{A})_l \\
&= \epsilon_{jkl} \dot{x}_k \epsilon_{lmn} \dfrac{\partial A_n}{\partial x_m} \\
&= (\delta_{jm} \delta_{kn} - \delta_{km} \delta_{jn})\dot{x}_k \dfrac{\partial A_n}{\partial x_m} \\
&= \dot{x}_k \left( \dfrac{\partial A_k}{\partial x_j} -\dfrac{\partial A_j}{\partial x_k} \right)
\end{align*}(just replace the dummy index $k \rightarrow i$), and putting $\nabla \times \mathbf{A} \equiv \mathbf{B}$ as well as $-\dfrac{\partial \phi}{\partial \mathbf{r}} \equiv \mathbf{E}$ gives\begin{align*}
Q_j = q (\dot{\mathbf{r}} \times \mathbf{B})_j + qE_j
\end{align*}i.e. the Lorentz force

it's easy for this example, in the case of cartesian coordinates, to see that the generalised force is nothing but the actual force $Q_j = \mathbf{F} \cdot \dfrac{\partial \mathbf{r}}{\partial x_j} = \mathbf{F} \cdot \mathbf{e}_j = F_j$.

 

[wrobel]

Let us recall a formula for a rigid body, Assume that the rigid body experiences a net force $\boldsymbol F$ and a torque $\boldsymbol M_A$ about a point $A$. The point $A$ belongs to the rigid body. Then
$$Q_i=(\boldsymbol F,\frac{\partial \boldsymbol v_A}{\partial \dot q_i})+(\boldsymbol M_A,\frac{\partial \boldsymbol \omega}{\partial \dot q_i})$$