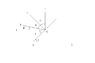How Do You Calculate the Angle for a Reflected Ray to Become Vertical?

  • Thread starter Thread starter Amith2006
  • Start date Start date
  • Tags Tags
    Inclined Mirrors
AI Thread Summary
To determine the angle y for which a reflected ray becomes vertical when a ray of light strikes an inclined mirror, the discussion outlines a calculation involving angles. The ray makes a 10-degree angle with the horizontal and reflects off a mirror inclined at angle y. The solution involves setting up the equation 2m + 10 = 90, leading to m being 40 degrees. Subsequently, it is concluded that y must also equal 40 degrees to satisfy the conditions of the problem. The calculations are presented as consistent with orthonormality.
Amith2006
Messages
416
Reaction score
2
Inclined mirror problem

Sir,
Please see if it is right.
1)A ray of light makes an angle of 10 degrees with the horizontal and strikes a plane mirror which is inclined at an angle y to the horizontal. What is the angle y for which the reflected ray becomes vertical?
I solved it in the following way:
Given that angle(CBF) = 90, angle(CBD) = 10, angle(DBE) = angle(EBF) = m
i.e. 2m + 10 = 90
m = 40
Now, y + 10 + 40 = 90
y = 40

Is it right?
 

Attachments

  • Opt 5.GIF
    Opt 5.GIF
    1.7 KB · Views: 534
Last edited:
Physics news on Phys.org
Yes I think this is correct...you can check that the angles are consistent with orthonormality once you have the values, yourself.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Diffraction Gratings: Calculating Wavelength for CD ROM
Replies
6
Views
2K
How to solve for angle of reflection in respect to floor?
Replies
5
Views
5K
What is the maximum reflection angle in the Chandra X-ray telescope optics?
Replies
8
Views
2K
How Do You Calculate the Maximum Angle of Inclination After a Collision?
Replies
10
Views
3K
Incline plane problem - acceleration, time, and velocity
Replies
1
Views
6K
What is the best shape for a soccer goal post?
4
Replies
157
Views
11K
Calculate tilt angle of a bar lifted via two ropes on fixed points
Replies
7
Views
3K
To find the centre of gravity of a lamina
Replies
2
Views
2K
How to find angle between two inclined plane mirrors?
Replies
4
Views
17K
Find min/max accel. for block to stay on wedge (static fric)
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top