Two objects on an incline with friction, calculate acceleration? B

[rover_dude]

Homework Statement

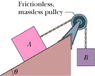
Body A in Fig. 6-33 weighs 97 N, and body B weighs 91 N. The coefficients of friction between A and the incline are μs = 0.48 and μk = 0.25. Angle θ is 47°. Let the positive direction of an x-axis be down the slope. What is the acceleration of A if A is initially (a) at rest, (b) moving up the incline, and (c) moving down the incline? Here is figure 6-33 http://edugen.wileyplus.com/edugen/cours…

I have tried multiple attempts but they have been wrong. Obviously I know part a) is zero, but I need help with parts b) and C).

Homework Equations

F=ma

The Attempt at a Solution

I have tried multiple attempts but they have been wrong. Obviously I know part a) is zero, but I need help with parts b) and C).

Here is my attempt for B)
Fx: F(friction) + mg*sin(47) - F(B on A)=0 With some reworking and addition of numbers I got F(B on A)=71.1913 I set that equal to ma (F=ma) where mass is 97/9.8 and divided 71.1913 by (97/9.8) to get a=7.1925, after i found that that wasn't right, I didn't try for part c) but the 7.1925 would be negative because of how the axis are set up.

Now that I look at it I realize that F(friction) + mg*sin(47) - F(B on A) would not be equal to zero because it would be moving but I don't know where to go. Thanks!

 

[NascentOxygen]

Document not found.

 

[rover_dude]

Here it is, sorry.

 

[daqddyo1]

Solution to part a).
Why do you think the acceleration will automatically be 0?
Try this “thought” experiment. Push and release a mass up a frictionless slope.
The mass slows down due to the component of gravity down the ramp. You could calculate the acceleration easily. At the instant the mass stops before sliding back down, is the acceleration 0? No it is not. Why? Because the component of gravity is still there. Ther is still an unbalanced (net) force acting.

In your question, the acceleration when the mass on the ramp is at rest will depend on whether the sum of the forces parallel to the ramp acting on that mass (Body A) is less than or greater than the static friction force acting on body A.
Once you have this figured out, you can determine the sum of the forces acting and the resulting acceleration.

 

[rover_dude]

Well, it is online homework so I put zero in and it is right, so, but thanks. I would just like an explanation for parts b and c because my professor does not do examples in class.

 

[daqddyo1]

For parts b) and c) imagine that the system of blocks A, B and the string are stretched out on a surface. You can do this because both masses will have the same acceleration whether we’re looking at this picture or at the masses in the given diagram (because the string always remains taught). This also means that the tension in the string is a red herring.

Draw a free body diagram showing the forces acting on this system.

For part b), choose the positive direction to be up the ramp. The force pulling right = the weight of mass B = +97 N. Since mass A is moving up the ramp, the forces acting to the left will be the kinetic friction on A and the component of gravity acting on mass A.
So, the force acting to the left will be -- 97sin47 – (97x0.25xcos47).

Add the 3 forces together to get the net force. Remember that the total mass accelerated is mass A + mass B. Calculate the acceleration.

For part c), you know the one force that has changed (in direction). Finish this part yourself.