Uncertainty Principle: L & Angular Position

[getcarter]

Verify that the uncertainty principle can be expressed in the form

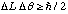, where

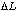is the uncertainty in the angular momentum of a particle, and

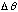is the uncertainty in its angular position. (You may think of a particle, mass m, moving in a circle of fixed radius r, with speed v)

b) At what uncertainty in L will the angular position of a particle become completely indeterminate?

 

[gabbagabbahey]

What have you tried? You need to show some sort of attempt to get assistance here as per forum policy.

 

[borgwal]

Once you have answered part (b), you will see that the relation that you're supposed to prove in part (a) cannot be quite correct!