- #1
johndb
- 24
- 0
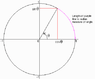
Problem understanding waves. I can see how rates of speed in circular motion can translate to expressed different kinds/shapes of waves but I don' see why concepts of trigonometry like sin,cos are brought into describing waves. I just feel there could be clearer ways of describing waves.