Understand Special Relativity and Time paradox

[bobc2]

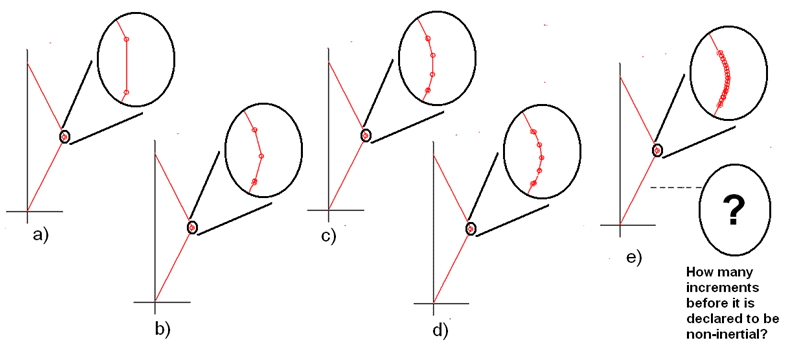
I get the impression that the concept of the sequence of inertial frames to represent the turnaround is not being understood. In the sketches below we show how you might represent a turnaround with more and more inertial frames. The number of inertial frames increases in each sketch, a) through e). A procedure such as one of these could be implemented with a rocket if you perform a sequence decelerations followed by a sequence of accelerations back toward the start point once the turnaround point is reached. Between each rocket impulse you would coast in an inertial frame during which the Lorentz transformations apply. You could break the turn-around incrementally into as many inertial frames as desired. Should there be any limit in smallness and number of the worldline increments used in the sequence of inertial frames? Of course not.

So, it is incorrect to regard this scenario as requiring a non-inertial analysis. This is nothing more than a generalization of the accepted practice of using a single turnaround point when analyzing the final age differences of the twins.

Further, the full extent of the Lorentz frames (including positive and negative directions) should be recognized. Again, that does not mean that the red observer's clock runs backwards (see previous post sketch), even though red worldline clock time are presented in the sequence of traveling twin's inertial frames as a sequence of clock times going backwards in time. That certainly does not mean that either the twin or the Red observer are actually moving backward in time. Both observers are moving along their respective worldlines at the speed of light.

 

[PeterDonis]

I get the impression that the concept of the sequence of inertial frames to represent the turnaround is not being understood.

I understand it just fine. I can't speak for DaleSpam and PAllen and others, but I suspect they understand it just fine as well. But you appear to be claiming that your analysis tells us something about "reality"--that there is some "real meaning" to the fact that the times assigned to events on red's worldline "appear to go backwards" in the succession of frames that blue uses. That's the claim that we are disagreeing with.

The times assigned by blue in the succession of frames you describe are just coordinate times; they don't have any physical meaning by themselves. If you try to translate them into statements that have physical meaning, i.e., into statements about invariants, you will find, of course, that the invariants regarding time, such as red's own proper time, "move forward" as expected. I say "of course" because you already know this, since you said so in a previous post.

 

[Dale]

The times assigned by blue in the succession of frames you describe are just coordinate times; they don't have any physical meaning by themselves.

I actually disagree with this slightly. They are not even coordinate times (on the red worldline) since they violate the one-to-one requirement of coordinate charts.

 

[Dale]

Should there be any limit in smallness and number of the worldline increments used in the sequence of inertial frames? Of course not.

So, it is incorrect to regard this scenario as requiring a non-inertial analysis. This is nothing more than a generalization of the accepted practice of using a single turnaround point when analyzing the final age differences of the twins.

You seem to think that a worldline single turnaround point is inertial. This is incorrect. Even one "increment" representing a sharp instantaneous acceleration is enough to make the traveling twin and his frame be non-inertial.

As long as the worldline is bent at all in an inertial frame then it is non-inertial. It does not matter if it is a single sharp bend, a gradual continuous bend, or a series of small sharp bends. The answer to your question "how many increments before it is declared to be non-inertial" is 1.

 

[PeterDonis]

They are not even coordinate times (on the red worldline) since they violate the one-to-one requirement of coordinate charts.

The time assigned by each individual frame in the succession of blue's frames is a coordinate time; the time assignments of each individual frame are one-to-one. The problem only arises if you try to put together a single non-inertial frame whose coordinate assignments along a given worldline (such as red's) agree with those of the succession of inertial frames; as you point out, you can't do that globally without violating the one-to-one requirement.

It looks to me like bobc2 didn't actually intend to construct a single non-inertial frame in this way, but to me that's really a side issue; even if one is careful *not* to make any claims about a single non-inertial frame, it's still true that you can't get anything physically meaningful just by looking at coordinate times of events along red's worldline in the succession of blue's inertial frames.

 

[bobc2]

The time assigned by each individual frame in the succession of blue's frames is a coordinate time; the time assignments of each individual frame are one-to-one. The problem only arises if you try to put together a single non-inertial frame whose coordinate assignments along a given worldline (such as red's) agree with those of the succession of inertial frames; as you point out, you can't do that globally without violating the one-to-one requirement.

It looks to me like bobc2 didn't actually intend to construct a single non-inertial frame in this way...

You are exactly correct. That is what I've been trying to get across. Regarding the collection of individual inertial frames as representing a single non-inertial frame is definitely not the way to understand this.

...but to me that's really a side issue; even if one is careful *not* to make any claims about a single non-inertial frame, it's still true that you can't get anything physically meaningful just by looking at coordinate times of events along red's worldline in the succession of blue's inertial frames.

That is a philosophically based idea. Einstein cautioned against these kinds of ideas which trap you into solipsism.

You are saying that there is no reality to be associated with the hyperplanes of simultaneity for a given Lorentz frame. I don't think our monitor will want us to continue a discussion along those lines. The monitor may allow you to define for us how you would describe or define criteria for identifying the real world of existence in the context of physical theory--I'm not sure.

 

[Dale]

The time assigned by each individual frame in the succession of blue's frames is a coordinate time; the time assignments of each individual frame are one-to-one. The problem only arises if you try to put together a single non-inertial frame whose coordinate assignments along a given worldline (such as red's) agree with those of the succession of inertial frames; as you point out, you can't do that globally without violating the one-to-one requirement.

Right, and this is exactly what bobc2 did in his post 32. In that post he is explicitly NOT talking about a sequence of individual 4D inertial frames, but a sequence of instantaneous "3D worlds". This is the same as defining a simultaneity convention for a single non-inertial 4D coordinate system.

 

[Dale]

You are exactly correct. That is what I've been trying to get across. Regarding the collection of individual inertial frames as representing a single non-inertial frame is definitely not the way to understand this.

I already addressed this in post 50, but that is exactly what you were doing in claiming that the red guy's time was going backwards. If you talk about a sequence of inertial frames then his clock goes forwards at all times and in all frames. If you talk about a sequence of "3D worlds" then you are talking about a 4D non-inertial frame, and mathematically that frame cannot cover the red guy's worldline.

That is a philosophically based idea. Einstein cautioned against these kinds of ideas which trap you into solipsism.

Reference please?

 

[PeterDonis]

Regarding the collection of individual inertial frames as representing a single non-inertial frame is definitely not the way to understand this.

Then, as DaleSpam pointed out, you can't make any claims about red's time "running backwards". Just noticing that the coordinate times in a succession of different inertial frames "run backwards" doesn't say anything about red's time "running backwards".

That is a philosophically based idea. Einstein cautioned against these kinds of ideas which trap you into solipsism.

Einstein did no such thing. Arguments from authority don't count anyway, but I believe Einstein would have agreed that coordinate times (and indeed coordinates in general) are not "physically real". See below.

The monitor may allow you to define for us how you would describe or define criteria for identifying the real world of existence in the context of physical theory--I'm not sure.

Read my post #49. I gave there a perfectly good definition of what counts as "real"--invariants, things that are not frame-dependent. As far as I know, as I said in that post, Einstein would have agreed with such a definition. Simultaneity is frame-dependent, hence it does not count as "real" by that definition. The same goes for coordinate times, and for your "3-D worlds". They are fine as logical constructions, or as elements in a model that helps you to understand things; but that's all.

 

[laurub]

No, your brother will not receive many messages from you at the moment of his about-face. His about-face will not cause him to receive any messages from you. What's going to happen is that for the first half of his trip, he will receive messages from you at a slower rate than he sends them (1/R as I said in my first post to you), then for the second half of his trip he will receive messages from you at a faster rate than he sends them (R).

So for your example of your brother traveling at 0.5c, we can use the Relativistic Doppler formula to calculate what R is:

√((1+β)/(1-β)) = √((1+0.5)/(1-0.5)) = √((1.5)/(0.5)) = √3 = 1.732

And 1/R is the reciprocal, 0.57735.

This means that he will see your yearly messages coming to him slower than his during the first half of the trip. In fact it will take 1.732 years before he sees your first message.

And for the last half his trip, he will see your messages arriving more often than once per year according to his clock. It will only take 0.57735 years between each of your messages.

Now without knowing how long the trip will take, we can average these two numbers:

(1.732+0.57735)/2 = 2.30935/2 = 1.154675

This is the final ratio of your two clocks when he returns. How ever many years it took him according to his clock, yours will be 1.154675 times that amount.

So let's say your brother travels away at 0.5c for 13 years and then takes 13 years to get back at the same speed. Here is a spacetime diagram to show what is happening according to your rest frame. I show you as a thick blue stationary line with dots every year and your messages going out as thin blue lines traveling at c. I show your brother as a thick black line traveling at 0.5c with black dots every year and his messages coming back to you as thin black lines:

Now let's see how the previous calculations based on Relativistic Doppler fit in with this diagram. First off, I said that the rate at which your brother receives your yearly messages take 1.732 of his years. Can you see that on the graph? For example, at about his year 12, just before he turns around, he is just receiving the message you sent at your year 7. Can you follow that? If we divide 12 by 7 we get 1.714 which is about right. (We don't expect it to be exact because he didn't receive your message exactly at his year 12.)

Furthermore, if you look at your year 12, you can see that you are just receiving his message from year 7. It's symmetrical.

Now you should be able to see that after he turns around, he starts receiving your messages faster than one per year. In fact, from about his year 19 (you'll have to count his dots) to when you meet at his year 26, he will have received your messages from year 18 to 30. That is a ratio of the differences of (26-19)/(30-18) = 7/12 = 0.583, close enough to 0.577.

And in a similar manner, you can see that from his year 14 (just after he turns around) until you meet (12 years of messages from him), you will see them from your year 23 to your year 30 (7 years) and the reciprocal ratio applies.

Now that we can look at a spacetime diagram, we can see that the reason why the two of you age differently is because your brother sees these two ratios for half of his total trip time each but you see the smaller ratio for three-quarters of the time and the higher ratio for just one-quarter of the time. This means you are seeing him age less for a longer time while he sees you age less for half the time.

The last thing we want to notice is that ratio of your final age difference is 30/26 or 1.1538, very close to the actual 1.154675. (Again, these numbers are not exact because we're eyeballing them off the diagram.) This ratio is the famous value of gamma which is also the time dilation factor which shows in the diagram as the ratio of the coordinate time for your brother compared to his actual time on his clock. Can you see that?

Now I want to show you what the exact same information presented in the first diagram looks like in two more diagrams based on the IRF's in which your brother is at rest, first during his outbound leg and then during his inbound leg. First the outbound leg:

Notice how your brother's time is not dilated during the outbound leg (because he is at rest) but yours is. Note also that he has to travel at a higher speed than 0.5c (look up "veloctiy addition" in wikipedia to see that this higher speed is 0.8c) when he turns around and therefore now has more time dilation than you have. Nevertheless, all the signals between the two of you continue to travel at c and arrive at exactly the same times according to your own clocks as they did before. Does this all make sense to you?

Finally the diagram for the IRF in which your brother is at rest during the inbound leg:

This is very similar to the previous diagram so I won't go into any more explanation except that I want to point out that when your brother turns around, in no case does that have any bearing on what you see, until some time later and even then, each diagram shows accurately what you actually see and what your brother actually sees during the entire scenario.

Any questions?

Awesome diagrams and explanation! thank you for this!

 

[ghwellsjr]

Awesome diagrams and explanation! thank you for this!

You're welcome.

And thanks for the feedback.

 

[ghwellsjr]

Thanks George! I mean, I really want to thank you, in all of the threads I've already posted here, I've never seen such a good and detailed answer as yours. I'm new in special relativity and you explained everything so carefully I could understood almost completely. I thought I had understood before, but I didn't know the explanation had nothing to do to what I suppose it was correct. There should be more guys like you here in PF. I want to thank everyone who answered this thread but the george's answer was phenomenal (at least for me). Now I think I'm startin g to understand special relativity.

You're very welcome and thanks for feedback.

And yes, I do have some questons, I would appreciate if you could help me again

How it would be the diagram if we take the referential frame as the whole trip of my brother (I mean, my brother is at rest in the whole time). I'm not being able to "close" the graphic. If my brother is a straight line, my lines can't be together as they are smaller than his. Is this right?

The problem with the type of diagram that you are asking for is that it would not be inertial because your brother is not inertial. Inertial, in the context of Special Relativity means that he would be traveling at a constant speed in a constant direction, in other words, not accelerating. That means that it is impossible to use the Lorentz Transformation process to get from one of the IRF's we already considered to a not-inertial frame in which your brother was always at rest.

Besides, I'm curious, why do you want to have such a diagram? What do you think it will tell you that you don't already know from studying anyone of the IRF diagrams?

 

[bobc2]

I already addressed this in post 50, but that is exactly what you were doing in claiming that the red guy's time was going backwards. If you talk about a sequence of inertial frames then his clock goes forwards at all times and in all frames. If you talk about a sequence of "3D worlds" then you are talking about a 4D non-inertial frame, and mathematically that frame cannot cover the red guy's worldline.

You are still not getting it. I am not saying the red guy's clock goes backward for the red guy sitting at rest in his own frame of reference (see sketch at the bottom of my post #32). The red guy always sees his clock moving forward as he moves along his world line in his positive X4 (time) direction.

But if you were to make a list of the RED clock readings in the order they are presented in the blue guy's frame each time he (blue--referring to my earlier sketch at the bottom of post #32) boosts to his next inertial frame, then you would see those clock readings getting smaller and smaller as blue advances along his worldline (with blue's own clock readings moving forward in time). So, each time blue is coasting in a new inertial frame you note the clock reading on the red worldline at the intersection of the blue X1 axis with the red worldline (you can of course calculate this using the Lorentz transformation between red and blue coordinates, where red's frame is the same as black's except displaced along the black X2 axis). And of course you will perform a new Lorentz transformation for each new period of blue coasting in a new inertial frame.

So, we are not trying to manufacture some single coordinate transformation for a curvalinear non-inertial frame at all. We could talk about using something like Rindler coordinates, etc., but that's not at all what I've been trying to convey.

Reference please?

Here are a couple of Einstein quotes on solipsism from The Library of Living Philosophers Volume VII – Albert Einstein: Philosopher-Scientist, Paul Arthur Schillp,Editor

I've included comments with a sketch to clarify the way the problem of solipsism comes into special relativity and hyperplanes of simultaneity.

Page 673 …A few more remarks of a general nature concerning concepts and [also] concerning the insinuation that a concept - for example that of the real - is something metaphysical (and therefore to be rejected). A basic conceptual distinction, which is a necessary prerequisite of scientific and pre-scientific thinking, is the distinction between "sense-impressions" (and the recollection of such) on the one hand and mere ideas on the other...one needs this distinction in order to be able to overcome solipsism… we shall make use of this distinction unconcerned with the reproach that, in doing so, we are guilty of the metaphysical "original sin."

Page 673 (further down the page) …We represent the sense-impressions as conditioned by an "objective" and by a "subjective" factor. For this conceptual distinction there also is no logical-philosophical justification. But if we reject it, we cannot escape solipsism.

Also from Schillp, Page 81: "Physics is an attempt conceptually to grasp reality as it is thought independently of its being observed. In this sense one speaks of 'physical reality'."

"Belief in an external world independent of the perceiving subject is the basis of all natural science."
Einstein, "Maxwell's Influence on the Evolution of the Idea of Physical Reality," 1931, in Einstein, Albert, Ideas and Opinions, New York: Random House, 266.

“I am not a positivist. Positivism states that what cannot be observed does not exist. This conception is scientifically indefensible, for it is impossible to make valid affirmations of what people 'can' or 'cannot' observe. One would have to say 'only what we observe exists', which is obviously false.
Autobiographical Notes, 1949, in Schilpp 1949 p.81

The sketch depicts the problem with denying the real external world does not exist for observers if they cannot observe it. A common objection to the external world existing for an observer at a particular moment in time is that he cannot know anything about such a world “out there” until light signals arrive to inform the observer—by then the external world he is informed of is in the distant past (such as observation of stars, etc.).

So, the problem as depicted below is that under such objections the observer cannot know of anything but himself, for he is continually advancing forward along his worldline at the speed of light at the apex of his backward light cone. At that apex point he has no knowledge of the world of his hyperplane of simultaneity, and by the positivist’s claim he must consider himself to be a solipsist—the only known existing entity.

 

[PeterDonis]

the observer cannot know of anything but himself, for he is continually advancing forward along his worldline at the speed of light at the apex of his backward light cone. At that apex point he has no knowledge of the world of his hyperplane of simultaneity, and by the positivist’s claim he must consider himself to be a solipsist—the only known existing entity.

Sorry to be blunt, but this is hogwash. The observer has information coming in from his past light cone, and that information tells him about the existence of other objects. The information is time-delayed, but so what? It's still perfectly good information about the existence of other objects.

Edit: On reflection, it's even worse than that. You (bobc2) are arguing for a "block universe" interpretation of SR. But on that interpretation, "objects" don't exist in 3-D worlds; they exist in 4-D spacetime. So knowledge of *any* event on an object's worldline counts as knowledge of the object's existence, since the object *is* its worldline. So not only are you incorrectly stating the opposing view, you aren't even consistently applying your own view.

 

[PeterDonis]

Here are a couple of Einstein quotes on solipsism from The Library of Living Philosophers Volume VII – Albert Einstein: Philosopher-Scientist, Paul Arthur Schillp,Editor

These are all general comments. How about some quotes where Einstein talked specifically about relativity? As in, where he said the same sorts of things I said in my post #49?

 

[Dale]

Here are a couple of Einstein quotes on solipsism

OK, those quotes all show that Einstein didn't like solipsism, which wasn't in doubt. Not one of them support your claim that Einstein said that rejecting the physical meaningfulness of coordinate time leads to solipsism.

 

[bobc2]

Sorry to be blunt, but this is hogwash. The observer has information coming in from his past light cone, and that information tells him about the existence of other objects. The information is time-delayed, but so what? It's still perfectly good information about the existence of other objects.

You have just made my case. What do you think I've been trying to get across all of this time? I've certainly not been claiming that there is no external world just because the observer is always moving at the apex of his light cone. That was my example of the absurdity you arrive at when denying the external world of the hyperplanes of simultaneity. You're the one who has been denying the reality of the real external objective world represented by the hyperplanes of simultaneity.

Edit: On reflection, it's even worse than that. You (bobc2) are arguing for a "block universe" interpretation of SR. But on that interpretation, "objects" don't exist in 3-D worlds

No. 1: I have said nothing of block universe. But, what an absurdity for you to come to the conclusion that objects don't exist in the 3-D world because they are 4-D objects. That's like saying a thin slice of a wooden 2 x 4 lumber doesn't exist because its length is 8 ft and the slice is only 0.001 inch thick. How does a 3-D piece of an object not exist just because it is a piece of a 4-D object. You have lost all logic here.

...they exist in 4-D spacetime. So knowledge of *any* event on an object's worldline counts as knowledge of the object's existence, since the object *is* its worldline. So not only are you incorrectly stating the opposing view, you aren't even consistently applying your own view.

Sorry to be blunt, but you have just presented a total distortion of what my posts have been conveying, and you logic is totally flawed. And, again, I've said nothing of block universe--I don't think the monitor wants any more of that.

 

[Dale]

You are still not getting it. I am not saying the red guy's clock goes backward for the red guy sitting at rest in his own frame of reference (see sketch at the bottom of my post #32). The red guy always sees his clock moving forward as he moves along his world line in his positive X4 (time) direction.

I understand that. You are talking about your take on the blue observer's "perspective". The problem is that the math simply doesn't support your claim.

But if you were to make a list of the RED clock readings in the order they are presented in the blue guy's frame each time he (blue--referring to my earlier sketch at the bottom of post #32) boosts to his next inertial frame, then you would see those clock readings getting smaller and smaller as blue advances along his worldline (with blue's own clock readings moving forward in time). So, each time blue is coasting in a new inertial frame you note the clock reading on the red worldline at the intersection of the blue X1 axis with the red worldline (you can of course calculate this using the Lorentz transformation between red and blue coordinates, where red's frame is the same as black's except displaced along the black X2 axis). And of course you will perform a new Lorentz transformation for each new period of blue coasting in a new inertial frame.

So, we are not trying to manufacture some single coordinate transformation for a curvalinear non-inertial frame at all. We could talk about using something like Rindler coordinates, etc., but that's not at all what I've been trying to convey.

That is exactly what you are trying to do. You are going to great linguistic lengths to disguise that fact, but it is exactly what you are trying to do.

You are adopting a simultaneity convention, and giving it an ordering corresponding to readings on a clock, so that clearly establishes a time coordinate. That time coordinate is not the time coordinate of an inertial frame, so your frame is non inertial.

All of your verbose obfuscations do not hide that fact. If you do not adopt a simultaneity convention and give it an ordering then you cannot claim that red's clock runs backwards according to blue. As soon as you do that, then you have established a non inertial frame.

 

[bobc2]

OK, those quotes all show that Einstein didn't like solipsism, which wasn't in doubt. Not one of them support your claim that Einstein said that rejecting the physical meaningfulness of coordinate time leads to solipsism.

DaleSpam, your not connecting the dots. The collection of Einstein quotes makes it quite clear the point Einstein was making about solipsism, and it is quite obvious that the external reality he refers to is associated with the hyperplanes of simultaneity. Can you imagine any other component of the Einstein-Minkowski model that could play that role in the description of physical reality?

I knew this would spiral into a monitor lockdown.

 

[Dale]

DaleSpam, your not connecting the dots.

If the dots have to be connected to make your point then it is not something Einstein actually said, is it?

It is one thing to claim that X leads to Y, but you are trying to give your claim a false veneer of authority. It is both fallacious and counter-factual. Einstein never said what you claim he said, and even if he did that doesn't make it correct.

it is quite obvious that the external reality he refers to is associated with the hyperplanes of simultaneity. Can you imagine any other component of the Einstein-Minkowski model that could play that role in the description of physical reality?

Yes, the invariants could play that role.

It is not obvious at all to me that he is referring to hyperplanes of simultaneity, and he certainly wasn't explicit about it. You are putting your own words in his mouth. I think that you need to re-read what he actually said and not insert your own biases.

 

[zonde]

OK, those quotes all show that Einstein didn't like solipsism, which wasn't in doubt. Not one of them support your claim that Einstein said that rejecting the physical meaningfulness of coordinate time leads to solipsism.

Well, not only solipsism but positivism too. For example this one:
“I am not a positivist. Positivism states that what cannot be observed does not exist. This conception is scientifically indefensible, for it is impossible to make valid affirmations of what people 'can' or 'cannot' observe. One would have to say 'only what we observe exists', which is obviously false."

And what you say sounds like positivism: "what cannot be observed does not exist".

 

[PeterDonis]

I've certainly not been claiming that there is no external world just because the observer is always moving at the apex of his light cone. That was my example of the absurdity you arrive at when denying the external world of the hyperplanes of simultaneity.

But in the block universe view, the "external world" is a single 4-D world. It is not a bunch of 3-D hyperplanes of simultaneity. The hyperplanes of simultaneity are completely unnecessary to the block universe view.

You're the one who has been denying the reality of the real external objective world represented by the hyperplanes of simultaneity.

I have been denying that hyperplanes of simultaneity are "real physical things" because they are frame-dependent, and "real physical things" are represented in the theory by frame-independent quantities. So far you have said absolutely nothing that refutes that view. I have certainly not been denying the reality of the "real external objective world"; I just deny that that real external objective world is represented by hyperplanes of simultaneity. And since that is precisely the point at issue, you can't help yourself to it by implying that "the real external objective world" *is* in fact represented by hyperplanes of simultaneity. You have to first *prove* that, and you haven't.

No. 1: I have said nothing of block universe.

Then what position, exactly, are you defending? I'm very confused.

But, what an absurdity for you to come to the conclusion that objects don't exist in the 3-D world because they are 4-D objects.

I said no such thing. What I have been saying is that "3-D worlds" are frame-dependent, and the actual physics of SR is contained in the things that are frame-independent, so the actual physics of SR is *not* contained in 3-D worlds. That in no way denies the "reality" of objects; the only things whose "reality" it denies are the 3-D worlds, and only in the sense that they are frame-dependent, so you don't need them to describe the physics.

That's like saying a thin slice of a wooden 2 x 4 lumber doesn't exist because its length is 8 ft and the slice is only 0.001 inch thick.

No, it's like saying that the 0.001 inch thick slice of the 8 ft. 2x4 is not the same thing as a complete slice out of the entire universe that contains the 0.001 inch thick slice of lumber.

How does a 3-D piece of an object not exist just because it is a piece of a 4-D object. You have lost all logic here.

I didn't say a 3-D piece of an object doesn't exist. See above for further elaboration of what I did say. Please read more carefully.

Sorry to be blunt, but you have just presented a total distortion of what my posts have been conveying

If you're not talking about the "block universe", then you're right, I have no idea what you think your posts have been conveying.

and you logic is totally flawed.

No, my logic is just not what you have been claiming it is.

And, again, I've said nothing of block universe--I don't think the monitor wants any more of that.

There's nothing wrong with talking about the block universe in itself. The only things that have gotten people in trouble are claims that the block universe is the only possible interpretation of SR.

 

[PAllen]

bobc2:

Still waiting for a reference where Einstein used hyperplanes' of simultaneity, or said that the point of view of a non-inertial observer matches that, moment to moment, of instantaneously comoving inertial frames. You claimed your approach matches Einstein's. I checked 4 papers Einstein treated non-inertial motion in SR, and none remotely resemble your approach. Still waiting for a reference on what you explicitly claimed - that your method matches Einstein's.

 

[PeterDonis]

If you're not talking about the "block universe", then you're right, I have no idea what you think your posts have been conveying.

bobc2, on re-reading the thread, I'm still not sure what you think your posts have been conveying, but perhaps I can help re-focus things a bit with a couple of questions.

First, the reason I assumed you were trying to defend a block universe interpretation is that I couldn't see any other reason for bringing in the 3-D worlds. If that wasn't meant as an argument for a block universe interpretation, what was it meant for?

Second, I see that this sub-thread more or less started with you adding the "red" observer's worldline to the spacetime diagram, and then observing that the coordinate times assigned to events on red's worldline "run backwards" in the succession of "blue" frames through the turnaround. What do you think that means? Why did you think it was important to make that observation?

 

[PAllen]

Please note further that the derivation of simultaneity convention for inertial observers relies on:

- being inertial long enough to apply a clock synchronization method (establishing simultaneity), for clocks a given distance apart. It is also preferred only in the sense that all reasonable methods agree.

- A non-inertial observer has a different past than co-moving inertial observer. This means that physical synchronization methods they might use will come out different from the comoving inertial frame. They also won't agree with each other.

I am not arguing solipsism. I think there is a meaningful sense in which inertial simultaneity convention (which is the one you are using) is preferred for inertial observers - for a volume of spacetime proportional to the time they have been effectively inertial. For a non-inertial observer it is not preferred or meaningful at all beyond a spacetime volume where, say, Einstein simultaneity and 'ruler' simultaneity differ to a detectible degree.

You want to give absolute meaning to a convention completely divorced from the way it was derived.

 

[ghwellsjr]

Bobc2, your Sketch III looks kind of like my first diagram in post #23 except that I have an instantaneous turn-around. The lines (or surfaces or volumes or whatever you want to call them) of simultaneity in my diagram are simply the horizontal grid lines (and the infinite number of horizontal lines in between them). In normal orthogonally drawn diagrams of IRF's, the issue of simultaneity is automatically handled by the grid lines and doesn't need any explanation. You don't show any equivalent grid lines either horizontally or vertically (or diagonally??) so it is very difficult for me to tell what is going on with your diagrams. I wonder if the OP is understanding them.

Secondly, I don't see any equivalent yearly messages traveling at c between the OP and his brother as he requested in post #13. Can you please put them in? And can you address his concern that a bunch of messages from him will arrive in a flood during his brother's about-face?

ghwellsjr, sorry I missed your post for a while there. I'll see if I can get back into this and respond to your questions sometime this weekend. Thanks.

The weekend is over. Can you please make the OP's requests a priority especially since you are concerned that the moderators are going to lock this thread?

 

[Dale]

And what you say sounds like positivism: "what cannot be observed does not exist".

Where did I say that? I don't know where you guys are getting this. Bobc2 with his strange obsession with solipsism and now you with positivism.

I am neither a solipsist nor a positivist. However, this is not a forum for philosophy of any kind, including philosophies that I agree with. This forum is for science, and I make a strong effort to keep it that way. I make a sincere effort not to promote my own philosophy and I try to discourage others from presenting theirs even when it happens to agree with mine.

I feel like there has been a weird revival of McCarthyism where people are randomly accused of being a solipsist or a positivist with no evidence to support the accusation.

 

[PeterDonis]

It is not obvious at all to me that he is referring to hyperplanes of simultaneity

It's fairly obvious to me, taking all of Einstein's writings on relativity into account, that he *wasn't*--that he was trying to focus attention on frame-independent things, not frame-dependent things. The particular quotes bobc2 gave, as I said before, are very general and don't even mention relativity specifically; when you look at what he actually wrote about relativity, it's clear that the "physical reality" he was talking about was represented in the theory by invariants, not by frame-dependent things like hyperplanes of simultaneity. His main emphasis on simultaneity is precisely to show that it is *relative*, i.e., to show that it is *not* the right thing to focus on.

 

[zonde]

However, this is not a forum for philosophy of any kind, including philosophies that I agree with. This forum is for science, and I make a strong effort to keep it that way. I make a sincere effort not to promote my own philosophy and I try to discourage others from presenting theirs even when it happens to agree with mine.

Philosophy is foundation of science. We can coherently talk about science as long as we agree about some philosophical foundations.

But if you are trying to put physics on different foundations then there is no way how we can avoid talking about philosophy.

And this idea about doing physics using invariants is attempt to put physics on different foundations.

 

[PAllen]

Philosophy is foundation of science. We can coherently talk about science as long as we agree about some philosophical foundations.

But if you are trying to put physics on different foundations then there is no way how we can avoid talking about philosophy.

And this idea about doing physics using invariants is attempt to put physics on different foundations.

Yes, invariants are the foundation of special and general relativity. Einstein several times said he wished the word relativity was never used - the theory should be called the theory of invariants. That is fundamentally the way it has been pursued since.

If you don't like this foundation, I guess you are left with physics of the 19th century.

 

[Mentz114]

Yes, invariants are the foundation of special and general relativity. Einstein several times said he wished the word relativity was never used - the theory should be called the theory of invariants. That is fundamentally the way it has been pursued since.

If you don't like this foundation, I guess you are left with physics of the 19th century.

Hear, hear. It is tiresome that so many 'objectors' base everything on the study of these old documents.

 

[PeterDonis]

Yes, invariants are the foundation of special and general relativity. Einstein several times said he wished the word relativity was never used - the theory should be called the theory of invariants. That is fundamentally the way it has been pursued since.

Exactly.

 

[Dale]

Philosophy is foundation of science.

I disagree completely. Experiment (scientific method) is the foundation of science and what distinguishes it from philosophy.

I cannot think of any philosophical proposition that has any scientific value except for those which are essentially restatements of Bayesian inference.

And this idea about doing physics using invariants is attempt to put physics on different foundations.

No, it isn't. The foundation of science is the scientific method. The scientific method requires that a theory make experimental predictions, but doesn't otherwise constrain the method of making those predictions. In relativity the experimental predictions of the theory are all invariants. No modification of the scientific method is necessary to do relativity using invariants.

 

[bobc2]

Exactly.

You have totally ignored the importance of Einstein's postulate about the laws of physics and different observer Lorentz frames.

 

[bobc2]

There seems to be confusion over the sequence of inertial frames associated with the traveling twin turnaround. I was simply pointing out what I thought was an interesting result for red clock readings as presented in the traveling twin’s sequence of inertial frames. So, here we will not be concerned about the period on the traveling twin's worldline during the turnaround. To avoid any further anguish over discretizing the turnaround, let’s just simplify the analysis by changing the focus away from the turnaround.

In the sketch below we show the same interesting feature by simply comparing readings on what I now show as the brown clock (red in the earlier sketch) as they are presented in the traveling twins two inertial frames, i.e., the purple frame (before turnaround) and the red frame (after turnaround). Notice that Event C presents a brown clock reading in the purple frame at the start of the outgoing trip of the traveling twin (the purple X1 axis represents the outgoing twin's simultaneous space at the start of his trip).

We show the beginning of the twin return trip as Event A (the traveling twin has just completed the turnaround and has started back home, i.e., the Red frame in the sketch). In this twin’s inertial frame the brown clock is presented on the worldline of the Brown frame as Event B.

When the traveling twin reaches Event D, the Event C is simultaneous with that same event (C simultaneous with D) in the twin’s inertial frame.

So, I am simply making the observation that as the traveling twin moves along his worldline, Event C is encountered at the start of the twin’s outgoing inertial frame before the Event B is encountered in the twin’s return inertial frame, even though as the Brown observer moves along his own X4 (time) axis, he (Brown) naturally experiences Event B before Event C. And Events D and C are simultaneous in the twin’s inertial frame. That’s all. No implications are drawn here—just an interesting observation for one to interpret however one pleases. Some may find nothing of interest here.

So far as the ability to connect the dots beginning with Einstein’s quotes about solipsism, I realized that many forum members may not be familiar with Bertrand Russell’s development of the concepts of sense impressions and ideas and their distinction. Einstein’s comments should be taken in that context. Russell devoted a lengthy discussion to this subject in his book. He develops this platform to launch the argument in support of an external objective reality. The argument between realists (such as Einstein) and idealists (a significant number of philosophers) has to begin on the turf of the inner experience, so that’s where Einstein has taken it up in the quotes presented earlier where he referenced the “objective” physical reality and asserted the logical conclusion that one who rejects this has “no escape from solipsism.” But it is just the logical beginning point for the analysis leading to refuting the positivist’s denial of the external reality out from the apex of an observer’s light cone. I don’t understand why connecting the dots should be that difficult. Einstein claimed emphatically that he was not a positivist.

Now, about invariants. You folks are corrupting the use of the concept to imply what was never intended. You completely ignore the significance of one of Einstein’s postulates: The laws of physics are the same for all frames (we understand this to mean Lorentz frames). The Lorentz inertial hyperplanes of simultaneity are exactly those for which Einstein’s postulate holds. This is fundamental in understanding the sequence of 3-D volumes (hyperplanes of simultaneity) as presenting the physical reality implied by special relativity.

 

[PeterDonis]

You have totally ignored the importance of Einstein's postulate about the laws of physics and different observer Lorentz frames.

Could you elaborate? I don't understand what point you're trying to make. The only "postulate" I can think of that you could be referring to is the one that says the laws of physics must be invariant under Lorentz transformations; that means the laws have to be written in terms of invariant expressions. That would seem to support what I've been saying.

 

[Mentz114]

Now, about invariants. You folks are corrupting the use of the concept to imply what was never intended. You completely ignore the significance of one of Einstein’s postulates: The laws of physics are the same for all frames. The Lorentz inertial hyperplanes of simultaneity are exactly those for which Einstein’s postulate holds. This is fundamental in understanding the sequence of 3-D volumes (hyperplanes of simultaneity) as presenting the physical reality implied by special relativity.

How would you express "The laws of physics are the same for all frames" without using frame independent concepts ? Nor do I believe "inertial hyperplanes of simultaneity are exactly those for which Einstein’s postulate holds". I think you may be confused.

 

[PeterDonis]

No implications are drawn here—just an interesting observation for one to interpret however one pleases. Some may find nothing of interest here.

In other words, this observation is irrelevant to the rest of the discussion? Fair enough; then I won't bother commenting further on it.

So far as the ability to connect the dots beginning with Einstein’s quotes about solipsism, I realized that many forum members may not be familiar with Bertrand Russell’s development of the concepts of sense impressions and ideas and their distinction. Einstein’s comments should be taken in that context.

I am familiar with Russell's writings on these concepts; the best exposition I know of is in Russell's book Our Knowledge of the External World. I have no problem with the general claims Russell makes in that book, and I would agree that the views Einstein expressed in general terms were similar. The basic idea is that, even if we start by only granting "existence" to our direct sense-impressions, we can't make sense of those sense-impressions without committing ourselves to the existence of an "external world".

However, the disagreement we're having is not about whether an external world exists; it's about *what*, specifically, we are entitled to claim "exists" based on a certain set of sense impressions--i.e., what, exactly, is the "external world" that we need to believe in in order to make sense of a given set of sense impressions. See further comments below.

But it is just the logical beginning point for the analysis leading to refuting the positivist’s denial of the external reality out from the apex of an observer’s light cone.

Nobody here is making a "positivist denial" of external reality. But you have assumed, without proof, that the sense impressions we receive from our past light cone *force* us to believe in an "external reality" consisting of an instantaneous 3-D world. That's simply not a valid claim. To see why, contrast it with the following alternative claim:

Based on the sense impressions we receive, we can only make sense of them by believing in the existence of external objects that send us light signals containing information about them. But the information we receive this way is time-delayed; for example, the Sun that I see is the Sun as it was eight minutes ago, *not* the Sun as it is "now". So the "external world" that I am *forced* to believe in based on my sense impressions does not include the Sun "now"; it only includes the Sun up to eight minutes ago.

I can, of course, make the further claim that, since it is highly unlikely that anything significant will have happened to the Sun in the eight minutes it took for the light I am seeing now from the Sun to get to me, it is highly probable that there is in fact a Sun now--i.e., that the Sun's worldline extends beyond the portion I have direct evidence of in my past light cone. But that is a *different* kind of claim from the claim that I have to believe in an external world based on my sense impressions. The claim that the Sun exists now is an *extrapolation* from the direct data in a way that the claim that the Sun existed eight minutes ago is not.

You completely ignore the significance of one of Einstein’s postulates: The laws of physics are the same for all frames. The Lorentz inertial hyperplanes of simultaneity are exactly those for which Einstein’s postulate holds.

Einstein's postulate says nothing about hyperplanes of simultaneity. Go look at the relativistic formulations of any law of physics--Maxwell's Equations, the Einstein Field Equations, quantum field theory--and tell me where in those laws the hyperplanes of simultaneity are.

 

[Dale]

So far as the ability to connect the dots beginning with Einstein’s quotes about solipsism, ... I don’t understand why connecting the dots should be that difficult.

It isn't about connecting dots. You claimed that Einstein said something that he simply did not say. You may believe that he meant to say what you claimed, or that what you claimed is implied by things that he said, but the unavoidable FACT is that he simply didn't say what you claimed he said.

Why don't you take ownership of your own opinions rather than trying to foist them off to Einstein? Say what you think, defend your ideas on their own merits, and simply leave Einstein out of it. Even where he shares your opinion, that is just a fallacious appeal to authority.

Now, about invariants. You folks are corrupting the use of the concept to imply what was never intended. You completely ignore the significance of one of Einstein’s postulates: The laws of physics are the same for all frames (we understand this to mean Lorentz frames).

The invariants are also the same for all frames, so I don't know what makes you think that we are ignoring the significance of the first postulate by focusing on them instead of frame-variant quantities.

 

[bobc2]

I'm really getting confused about what your fundamental objections are aside from the side bars on interpretations and philosophy.

Are you claiming that Event C is not in the traveling twin's simultaneous space at the start of his journey?

Are you claiming that Events A and B are not in the simultaneous space of the twin just after he has completed his turnaround?

Are you claiming that Events D and C are not in the simultaneous space of the twin when the twin has arrived on his worldline at Event D?

 

[PAllen]

I object to giving any physical meaning to simultaneous space. Simultaneity is a convention. For inertial observers (or in an inertial frame used to analyze some overall scenario), there is a standard convention any reasonable person would use; how far it makes sense to extend it (for an observer) depends on how long they have been inertial. For non-inertial observers there is no preferred convention except 'locally'. A non-inertial observer is analogous to the GR situation - only local frames (with standard simultaneity convention reasonably preferred sufficiently locally in time and space).

I believe this is how Einstein viewed it, but that is neither here nor there.

[There is also the sense of relatively arbitrarily chosen simultaneity surfaces used to construct coordinates useful for some problem. Obviously, I don't consider coordinates a feature of physical reality.]

 

[PeterDonis]

I'm really getting confused about what your fundamental objections are

I'm not objecting to any of the statements you have made about what events are in which simultaneous spaces. If those statements are all you've been trying to say, they strike me as too obvious to be worth taking all this time over.

aside from the side bars on interpretations and philosophy

The sidebars are only there because you have made claims about the interpretation and philosophy of simultaneous spaces. If you would refrain from making such claims we wouldn't need any sidebars.

If you had said things like "I find that looking at hyperplanes of simultaneity helps me to make sense of what is going on" (which is pretty much what LastOneStanding said right before you entered the thread to support what he was saying), I doubt we would have had any sidebars. But you insist on saying things like "hyperplanes of simultaneity are fundamental to relativity", which implies (incorrectly) that they are necessary to *any* understanding of relativity, and then claiming that Einstein said so too, which is a strained (at best) interpretation of what he said.

 

[bobc2]

The weekend is over. Can you please make the OP's requests a priority especially since you are concerned that the moderators are going to lock this thread?

ghwellsjr, I have searched through most of my Einstein writings and must concede that I'm not able to find the reference that I am recalling. Of course there is the possibility that I am mistaken in my recollection, so I'll just have to retract my reference to Einstein discretizing the turnaround into incremental boosts (incremental inertial frames) as I've been describing. Of course the concept is not original with me. You were right to have challenged that. If I ever do come up with it I'll let you know.

By the way, you did a very excellent job of explaining the doppler approach. I've read a number of accounts of this, most recently Paul Davies's discussion, and yours is as good as any and better than most--particularly with your use of the diagrams.

 

[bobc2]

I object to giving any physical meaning to simultaneous space. Simultaneity is a convention. For inertial observers (or in an inertial frame used to analyze some overall scenario), there is a standard convention any reasonable person would use; how far it makes sense to extend it (for an observer) depends on how long they have been inertial. For non-inertial observers there is no preferred convention except 'locally'. A non-inertial observer is analogous to the GR situation - only local frames (with standard simultaneity convention reasonably preferred sufficiently locally in time and space).

I believe this is how Einstein viewed it, but that is neither here nor there.

[There is also the sense of relatively arbitrarily chosen simultaneity surfaces used to construct coordinates useful for some problem. Obviously, I don't consider coordinates a feature of physical reality.]

I guess I just don't catch on to your thinking about how to describe external objective reality with objects moving about in space and time without the use of coordinates. And particularly when we need to select the particular coordinate transformations of the Lorentz group if we are to be assured of physical processes unfolding in the various observer spaces in a manner consistent with the laws of physics.

 

[bobc2]

I'm not objecting to any of the statements you have made about what events are in which simultaneous spaces. If those statements are all you've been trying to say, they strike me as too obvious to be worth taking all this time over.

That's all I'm trying to say. Forum members can muse over any possible implications about the simultaneous spaces with regard to physical reality if they are so inclined. In any case I thought the way the order of the brown clock readings, as they are presented in the traveling twins's frames, was kind of interesting after Vandam had pointed it out in another thread (where is Vandam--he was so pasionate about this stuff?). Others may find nothing of interest there. I never intended to get side tracked into the philosophy of solipsism when I first posted--I tried to keep up with responses to new comments and questions but was inexorably drawn into the sid bars.

 

[Nugatory]

I guess I just don't catch on to your thinking about how to describe external objective reality with objects moving about in space and time without the use of coordinates.

It can be done. Any physical situation can be described in terms of proper time along timelike worldlines and the points at which these worldlines intersect lightlike null worldlines.

However, coordinates are a really really convenient calculating tool in many problems... So we use them a lot.

 

[Dale]

I guess I just don't catch on to your thinking about how to describe external objective reality with objects moving about in space and time without the use of coordinates.

Think about different ways you can describe the location of your house. You can give its latitude and longitude. Alternatively you could give some landmarks e.g. 2.3 miles past the post office on Balderdash Rd.

And particularly when we need to select the particular coordinate transformations of the Lorentz group if we are to be assured of physical processes unfolding in the various observer spaces in a manner consistent with the laws of physics.

The thing is that we already know experimentally that physical processes don't in fact transform according to the Poincare group globally, only locally. So we need to write the laws of physics in a manner that is consistent with completely arbitrary coordinate transforms because we know that the Lorentz transforms don't work globally.

Since we need to do that globally anyway, we can also do it locally. We then clearly see that the laws of physics don't care one bit what coordinate systems we use, and the actual laws of physics are expressed entirely in terms of invariant quantities.

 

[PeterDonis]

I never intended to get side tracked into the philosophy of solipsism when I first posted--I tried to keep up with responses to new comments and questions but was inexorably drawn into the sid bars.

I agree that your first post in this thread (#32, unless I missed something) didn't do anything more than draw the simultaneity planes in different frames and comment on them. But your next post (#34) used the word "fundamental":

I certainly have no fuss about doppler. Any special relativity course would not be complete without understanding that. But the real fundamental stuff of special relativity is intimately related to the time dilation, length contraction and hyperplanes of simultaneity as manifest in the Lorentz transformations and the space-time diagrams.

If you had qualified this with "for me", or "in at least one common method of teaching SR", it would have been different. But you made a blanket statement about what's "fundamental", which comes across as being about something more than just what works best when teaching or explaining.

Then, in post #38, you made the statement that I first responded to:

The attempt to replace the direct Lorentz based relativity of simultaneity with the doppler approach is just an argument based on philosophical ideas.

Again, if you had said "I find it much easier to understand and explain SR using relativity of simultaneity, etc., vs. doppler" that would have been different. But you brought in the "philosophical ideas" (that word had only been used once in this thread before your post, and nobody picked up on that one, by LastOneStanding).

 

[zonde]

I disagree completely. Experiment (scientific method) is the foundation of science and what distinguishes it from philosophy.

Discussions about scientific method are philosophy. Improvements in scientific method like falsifiability are philosophy.

The foundation of science is the scientific method. The scientific method requires that a theory make experimental predictions, but doesn't otherwise constrain the method of making those predictions.

Yes

In relativity the experimental predictions of the theory are all invariants.

Can you elaborate on this? First, is invariant defined or is it undefined basic concept?
Because the way it is usually defined i.e. some quantity that does not change under coordinate transformation, is confusing as it is defining invariants using concept of coordinates and consequently coordinate dependant quantities that we are using to construct coordinates. So coordinate dependant quantities are more basic than invariants.

The invariants are also the same for all frames, so I don't know what makes you think that we are ignoring the significance of the first postulate by focusing on them instead of frame-variant quantities.

Invariants are not the same as physical laws. They are certainly two different things.

 

[PAllen]

I guess I just don't catch on to your thinking about how to describe external objective reality with objects moving about in space and time without the use of coordinates. And particularly when we need to select the particular coordinate transformations of the Lorentz group if we are to be assured of physical processes unfolding in the various observer spaces in a manner consistent with the laws of physics.

I don't say you don't use coordinates. But they are analogous to the lines you draw on a globe to label positions. The globe and relief features on it exist independently of what lines I draw. Coordinates are not an aspect of reality. The Lorentz group is simply the group of transforms that preserve the flat space metric in simplest form. The physical principle of relativity is that absolute (inertial) motion cannot be detected. The difference from Galilean relativity is that light speed is included in what is the same for every inertial observer. There is nothing more special about Minkowski coordinates than there is about Cartesian coordinates on a plane (metric is in simplest form). Its geometry is there with no coordinate labels; if I draw polar coordinates, the geometry hasn't changed, only the process of computing things.

Your claim about some preferred meaning to your chosen 'simultaneity space' is equivalent to insisting that only cartesian coordinates are valid on a plane. Even more, that if we draw some arbitrary curve on a plane, and then want treat it as a coordinate axis, we must use lines perpendicular to its tangent at each point.