Understanding Convection Heat Transfer in a Convection Heat Exchanger

[Joshua Pham]

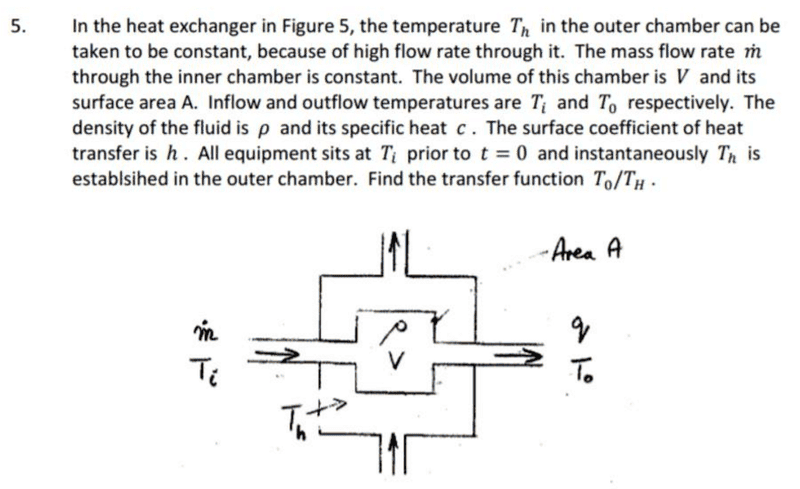
Hello guys, in the question attached, my understanding is that there is a heat transfer

that heats the fluid from an initial

at the input, to

at the output. This heat transfer is via convection from walls of temperature

.
Firstly,

.

Because the walls are

and the fluid is of a lower temperature, this heat transfer is via convection from the walls. The correct answer says that

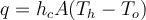. Why is this? Why not

? or

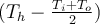. The fluid next to the wall is heated and changes until it reaches

at the outlet, so how do we know which temperature to use in the convection equation where heat is being transferred from the walls to the fluid?

 

[Chestermiller]

They expect you to assume that the overall heat transfer coefficient is h.

 

[Joshua Pham]

Hello Chestermiller; really apologise I didn't fill out the homework template. What does the over heat transfer coefficient $h_c$ have anything to do with the temperature difference being $T_h - T_o$? I would argue that the temperature difference used in $q = h_c A \Delta T$ should be $T_h - T_{average\ inside}$?

 

[Joshua Pham]

The heat flux is equal to the overall heat transfer coefficient times $(T_h-T_0)$ (i.e., the overall temperature difference).

I'm still not quite convinced. Why would $T_h - T_0$ be the overall temperature difference?? Would the "overall" temperature difference be the average temperature difference? Which is $$T_h - \frac{T_0 - T_i}{2}$$ ?

 

[Chestermiller]

Oh. I see what you are getting at. It goes like this:
$$\rho V c\frac{dT_0}{dt}=\dot{m}c(T_i-T_o)+hA(T_h-T_0)$$
This assumes that the chamber is well-mixed so that the average temperature in the chamber $T_0$ is always equal to the outlet temperature. So this is a transient heat transfer problem, in which you are solving for the average/outlet temperature as a function of time. So, at any given time, $T_0$ is assumed to be the temperature thorughout the chamber.

 

[Joshua Pham]

Ah! Thanks so much!

 

[Joshua Pham]

Hey Chestermiller, could you provide more insight into how you derived that equation? Reading online I've only seen the expression $$Ah(T-T_{\infty}) = -\rho Vc \frac{dT}{dt}$$ after googling transient heat convection transfers.

 

[Chestermiller]

Hey Chestermiller, could you provide more insight into how you derived that equation? Reading online I've only seen the expression $$Ah(T-T_{\infty}) = -\rho Vc \frac{dT}{dt}$$ after googling transient heat convection transfers.

This is the same as the equation I wrote, except for the term involving flow into and out of the chamber (which was not a feature of the problem in your reference).

 

[Joshua Pham]

This is the same as the equation I wrote, except for the term involving flow into and out of the chamber (which was not a feature of the problem in your reference).

Thanks Chestermiller.
The way I derived your expression is,
$$\dot{Q_{in}} - \dot{Q_{out}} = \frac{d(mc(T_o - T_i))}{dt}$$
but there is no $\dot{Q_{out}}$ if you consider the inner chamber as the system and there is no heat loss to the surroundings. So,
$$\dot{Q_{in}} = \frac{d(mc(T_o - T_i))}{dt}$$
Next, this heat transfer rate can only come from convection of heat from the walls interfacing the inner and outer chambers which is given by,
$$ q = h_cA(T_h - T_o)$$
These must equal and thus,
$$ \frac{d(mc(T_o - T_i))}{dt} = h_c A(T_h - T_o)$$
Now to obtain your expression, you need to subject the left term to the product rule. But why?? Aren't $T_i$ and $T_o$ constants? When I did a thermodynamics course, that left term would just turn into, $$\dot{m}c(T_o - T_i)$$

 

[Chestermiller]

Thanks Chestermiller.
The way I derived your expression is,
$$\dot{Q_{in}} - \dot{Q_{out}} = \frac{d(mc(T_o - T_i))}{dt}$$
but there is no $\dot{Q_{out}}$ if you consider the inner chamber as the system and there is no heat loss to the surroundings. So,
$$\dot{Q_{in}} = \frac{d(mc(T_o - T_i))}{dt}$$
Next, this heat transfer rate can only come from convection of heat from the walls interfacing the inner and outer chambers which is given by,
$$ q = h_cA(T_h - T_o)$$
These must equal and thus,
$$ \frac{d(mc(T_o - T_i))}{dt} = h_c A(T_h - T_o)$$
Now to obtain your expression, you need to subject the left term to the product rule. But why?? Aren't $T_i$ and $T_o$ constants? When I did a thermodynamics course, that left term would just turn into, $$\dot{m}c(T_o - T_i)$$

You must have forgotten a lot from your thermo course. For the material in the tank, m and c are constants, as is $T_i$ (but not $T_0$, of course, which is a function of time). You left out the terms for enthalpy flowing into and out of the tank.

Do you remember the open system (control volume) version of the 1st law of thermodynamics (that you must have learned in your thermodynamics course)? If so, please write it down for me.

Chet

 

[Joshua Pham]

You must have forgotten a lot from your thermo course. For the material in the tank, m and c are constants, as is $T_i$ (but not $T_0$, of course, which is a function of time). You left out the terms for enthalpy flowing into and out of the tank.

Do you remember the open system (control volume) version of the 1st law of thermodynamics (that you must have learned in your thermodynamics course)? If so, please write it down for me.

Chet

$$\dot{Q} - \dot{W} = \sum_{out} \dot{m} (h+ke+pe) -\sum_{in} \dot{m} (h+ke+pe) $$
Hence,
$$\dot{Q} = \sum_{out} \dot{m} h -\sum_{in} \dot{m} h $$

So for convection,
$$hA_c(T_h - T_o) = \dot{m}(h_2-h_1) = \dot{m}c_p(T_o-T_i)$$?

Why would $T_i$ be a constant but not $T_o$??

 

[Chestermiller]

$$\dot{Q} - \dot{W} = \sum_{out} \dot{m} (h+ke+pe) -\sum_{in} \dot{m} (h+ke+pe) $$
Hence,
$$\dot{Q} = \sum_{out} \dot{m} h -\sum_{in} \dot{m} h $$

So for convection,
$$hA_c(T_h - T_o) = \dot{m}(h_2-h_1) = \dot{m}c_p(T_o-T_i)$$?

This is the steady state version. You are dealing with a transient problem. So you have to include the rate of change of internal energy within the control volume (chamber).

 

[Joshua Pham]

This is the steady state version. You are dealing with a transient problem. So you have to include the rate of change of internal energy within the control volume (chamber).

Ah! Sorry

Here goes,
$$\dot{Q} + \dot{m}(h_1 - h_2) = \dot{m}(u_2 - u_1)$$

Heat is from convection so,
$$hA_c(T_h-T_o) = \dot{m}(c_p + c_v)(T_o-T_i)$$

Is that correct?
Why would $T_i$ be a constant but not $T_o$?

 

[Chestermiller]

Ah! Sorry

Here goes,
$$\dot{Q} + \dot{m}(h_1 - h_2) = \dot{m}(u_2 - u_1)$$

Heat is from convection so,
$$hA_c(T_h-T_o) = \dot{m}(c_p + c_v)(T_o-T_i)$$

Is that correct?

No. The rate of change in internal energy for the chamber is incorrect. It is $$\rho V\frac{du}{dt}=\rho Vc\frac{dT_0}{dt}$$
Also note that, for an incompressible liquid, the heat capacities at constant volume and pressure are the same, and are equal to the parameter c in your problem statement.

Why would $T_i$ be a constant but not $T_o$?

$T_i$ is the initial temperature, and also the temperature of the inlet stream to the chamber which, according to the problem statement is constant. $T_0$ is the temperature of the liquid inside of the chamber, and also the temperature of the liquid coming out of the chamber. The liquid is being heated, so its temperature is getting higher.

 

[Joshua Pham]

No. The rate of change in internal energy for the chamber is incorrect. It is $$\rho V\frac{du}{dt}=\rho Vc\frac{dT_0}{dt}$$
Also note that, for an incompressible liquid, the heat capacities at constant volume and pressure are the same, and are equal to the parameter c in your problem statement.

$T_i$ is the initial temperature, and also the temperature of the inlet stream to the chamber which, according to the problem statement is constant. $T_0$ is the temperature of the liquid inside of the chamber, and also the temperature of the liquid coming out of the chamber. The liquid is being heated, so its temperature is getting higher.

Thank you for that! I understand it much better now! In my thermo course, I think we just used steam tables for pure substances and the ideal gas equation for air. So I'd never dealt with a situation where the temperature was a function of time. I'm doing a second course later this year which will cover that. This is from a linear systems course.