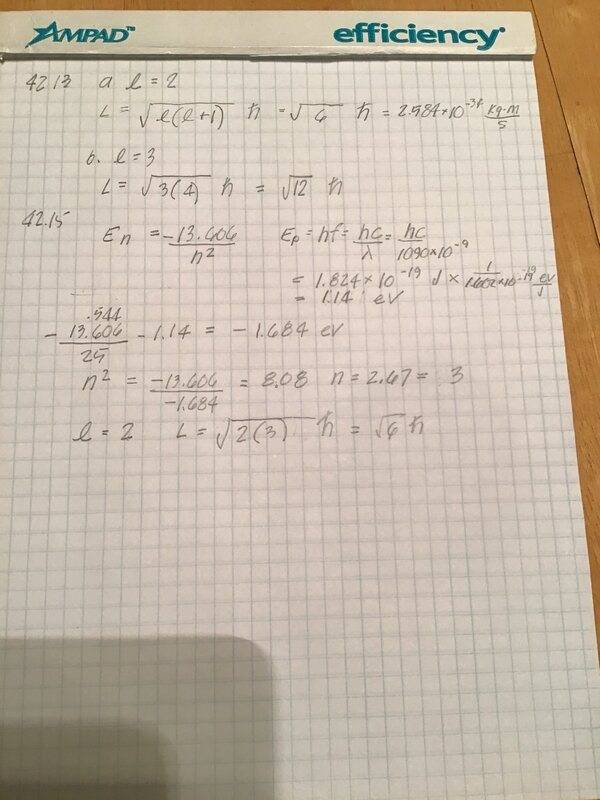Understanding Energy Conservation in Quantized Angular Momentum Transitions

Click For Summary
SUMMARY

The discussion centers on energy conservation in quantized angular momentum transitions, specifically regarding atomic energy levels and photon interactions. The energy of an atom at the principal quantum number n=5 is -0.544 eV, while the energy of the emitted photon is 1.14 eV. The calculation of the atom's energy post-emission results in a value of 1.68 eV, leading to confusion as it does not correspond to an integer quantum number. The correct interpretation of quantum states is crucial to avoid miscalculations in energy transitions.

PREREQUISITES
  • Understanding of quantum mechanics principles
  • Familiarity with atomic energy levels and quantum numbers
  • Knowledge of photon energy calculations
  • Experience with energy conservation laws in physics
NEXT STEPS
  • Study the concept of quantized energy levels in hydrogen-like atoms
  • Learn about the relationship between photon energy and frequency using the equation E=hf
  • Explore the implications of energy conservation in quantum transitions
  • Investigate the significance of principal quantum numbers in atomic structure
USEFUL FOR

Students and professionals in physics, particularly those focusing on quantum mechanics, atomic theory, and energy conservation principles.

jjson775
Messages
112
Reaction score
26
Homework Statement
42.15 A hydrogen atom is it its 5th excited state. The atom emits a 1 090 nm wavelength photon. Determine the maximum possible orbital angular momentum of the electron after emission.
Relevant Equations
En = -13.606/h^2
E = hf
I don’t understand how energy is conserved here. The energy of the atom when n=5 is -.544eV. The energy of the photon is 1.14eV. After release, the energy of the atom is -.544 - 1.14 = 1.68eV. Using this value, I get n = 2.67, not an integer, so n = 3 and the atom has energy = -1.51 eV. I have the right answer but am missing something basic.
IMG_0282.jpeg
 
Physics news on Phys.org
It's easy to slip up by taking n = 5 to correspond to the 5th excited state.
 
  • Like
Likes   Reactions: vela
TSny said:
It's easy to slip up by taking n = 5 to correspond to the 5th excited state.
It sure was!
 
  • Like
Likes   Reactions: TSny

Similar threads

Angular momentum for a bullet and a rod attached to a ceiling
  • · Replies 17 ·
Replies
17
Views
2K
Angular Momentum- Conserved or not?
  • · Replies 17 ·
Replies
17
Views
1K
Problem in understanding angular momentum of a rigid body
  • · Replies 10 ·
Replies
10
Views
2K
What Causes the Loss of Mechanical Energy in a Frictionless Spinning Cylinder?
  • · Replies 6 ·
Replies
6
Views
1K
To find the angular momentum of a disc
  • · Replies 50 ·
2
Replies
50
Views
4K
Conservation of angular momentum and rotational kinetic energy
  • · Replies 2 ·
Replies
2
Views
1K
Moment of inertia, conservation of angular momentum and energy
  • · Replies 5 ·
Replies
5
Views
1K
Perfectly inelastic collision between Projectile and a hinged disk
  • · Replies 26 ·
Replies
26
Views
2K
Is there a proof about angular momentum conservation?
  • · Replies 5 ·
Replies
5
Views
2K
Solving Orbital Speed with Energy & Angular Momentum Conservation
  • · Replies 7 ·
Replies
7
Views
3K