Understanding Line Integrals: Scalar vs Vector Fields

[cshum00]

Well i know that the line integral is

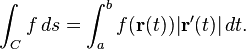given a scalar function f. equation1

But the line integral is also

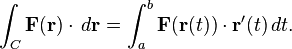given a vector field F. equation2

So, given scalar function f and taking the gradient vector of it in order to turn it into a vector field F. Why is equation1 not equal to equation2?

 

[HallsofIvy]

It's not clear to me what you are asking. If $F(r)= \nabla f$ then it is certainly true that $\int_C \nabla F\cdot dr= \int_a^b \nabla F(r)\cdot r'(t)dt$. But I don't know what you mean by "equation1 equal to equation2".

 

[cshum00]

Given $\nabla f = F(r)$
$\int_a^b f(r(t)) |r'(t)|dt \neq \int_a^b F(r(t)) \cdot r'(t)dt$
Why?

 

[HallsofIvy]

Given $\nabla f = F(r)$
$\int_a^b f(r(t)) |r'(t)|dt \neq \int_a^b F(r(t)) \cdot r'(t)dt$
Why?

Why should $\int_a^b f(r(t)) |r'(t)|dt \neq \int_a^b \nabla f(r(t)) \cdot r'(t)dt$?

 

[cshum00]

Well, let's try some example:

Let $f(x,y) = xy$
$F=\nabla f(x,y)=<y,x>$

Curve C => $y=x, 0<x<1$
Parametrize $r(t)=<t,t>, 0<t<1$
$r'(t)=<1,1>$
$|r'(t)|=\sqrt2$

$f(r(t))=t^2$
$F(r(t))=<t,t>$

If $\int_a^b f(r(t))|r'(t)|dt = \int_a^b F(r(t)) \cdot r'(t)dt$
$\int_0^1 t^2 \sqrt2dt = \int_0^1 <t,t> \cdot <1,1>dt$
$(\sqrt2/3) t^3 |_0^1 = \int_0^1 2t dt$
$\sqrt2/3 = t^2 |_0^1$
$\sqrt2/3 \neq 1$

 

[cshum00]

The only reason i have been asking this:
$\int_a^b f(r(t)) |r'(t)|dt \neq \int_a^b \nabla f(r(t)) \cdot r'(t)dt$
is because the formula given on the book say that they should be equal. However, as i try many examples; i never get the same answer. Here is some general proof i have been trying but never got far.

Let $f(x,y)=f(x,y)$
$F = \nabla f(x,y)=<f_x, f_y>$

Let Parametrization of Curve C:
$r(t) = <g(t), h(t)>$
$r'(t) = <g'(t), h'(t)>$
$|r'(t)| = [g'(t)^2 + h'^2(t)]^\frac{1}{2}$

$\int_a^b f(r(t)) |r'(t)|dt = \int_a^b \nabla f(r(t)) \cdot r'(t)dt$
$\int_a^b f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2}dt = \int_a^b <f(_x, f_y> \cdot <g'(t), h'(t)>dt$
$\int_a^b f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2}dt = \int_a^b g'(t)f_x(g(t), h(t))+ h'(t)f_y(g(t), h(t))dt$Since limits and variable of integration are the same then
$f(g(t), h(t))[g'(t)^2 + h'(t)^2]^\frac{1}{2} = g'(t)f_x(g(t), h(t)) + h'(t)f_y(g(t), h(t))$
But since i don't have any idea of what is going on inside those partial derivatives, i don't have a clue how to proceed.

Edit: In addition, the right hand side kind of looks like the product rule of a derivative.