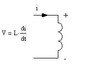the_kool_guy
- 37
- 0
i generally get confused in polarities of inductors and capacitors while doing KVL.
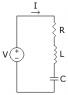
eg about a series RLC circuit ,the equation turns out to be ( Ldi/dt + iR + Vc = 0 )
this is the equation about assumed 'i' if we assume both capacitor and inductor in charging mode...
...
what if I assume inductor is discharging...then how can i reach the above equation...?
similar problem happens to me with circuits having only 1 active component...
.
.
.
can anyone enlighten me on this ..?
thanks
eg about a series RLC circuit ,the equation turns out to be ( Ldi/dt + iR + Vc = 0 )
this is the equation about assumed 'i' if we assume both capacitor and inductor in charging mode...
...
what if I assume inductor is discharging...then how can i reach the above equation...?
similar problem happens to me with circuits having only 1 active component...
.
.
.
can anyone enlighten me on this ..?
thanks