xtrubambinoxpr
- 86
- 0
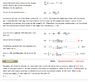
Homework Statement
in Attachment
Homework Equations
I = .5*mr^2
The Attempt at a Solution
I have no idea what is going on. This is a pre section quiz and I guessed on one and got it right. I don't know what is meant by the equations not giving I. I googled and noticed I has various equations. I plugged in the one I though most pertinent but it was marked wrong. Someone assist me please!