- 9,699
- 11,496
hi gang,
from wikipedia...
Mathematically, terminal velocity — without considering the buoyancy effects — is given by
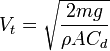
where
Vt = terminal velocity,
m = mass of the falling object,
g = acceleration due to gravity,
Cd = drag coefficient,
ρ = density of the fluid through which the object is falling, and
A = projected area of the object.
how do I know what the drag coefficient is ?
I realize air density depends on temperature and pressure and it changes throughout a column on atmosphere.
when a given Vt is quoted for an object ... are they just averaging the air density over the
"drop path" ?
cheers
Dave
from wikipedia...
Mathematically, terminal velocity — without considering the buoyancy effects — is given by
where
Vt = terminal velocity,
m = mass of the falling object,
g = acceleration due to gravity,
Cd = drag coefficient,
ρ = density of the fluid through which the object is falling, and
A = projected area of the object.
how do I know what the drag coefficient is ?
I realize air density depends on temperature and pressure and it changes throughout a column on atmosphere.
when a given Vt is quoted for an object ... are they just averaging the air density over the
"drop path" ?
cheers
Dave