Understanding the Effect of Perpendicular Components in Simple Harmonic Motion

AI Thread Summary
In the discussion, the focus is on the effect of perpendicular components in simple harmonic motion (SHM), specifically regarding the velocity components vcosθ and vsinθ. It is clarified that the component vsinθ, being perpendicular to the OY axis, does not influence motion along YOY', leading to confusion about its role in SHM. Participants debate whether the scenario represents circular motion instead of SHM, emphasizing the importance of angular velocity in SHM representation. The mention of missing elements in the provided diagram suggests a need for clearer visual aids to support understanding. Overall, the conversation highlights the relationship between perpendicular components and their impact on motion in SHM.
logearav
Messages
329
Reaction score
0

Homework Statement



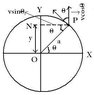
Kindly go through the attachment.
(i) vcosθ in a direction parallel to OY.

(ii) vsinθ in the direction perpendicular to OY.

The component vsinθ has no effect along YOY' since it is perpendicular to OY
My doubt is "Why the perpendicularity of vsinθ to OY makes vsinθ to have no effect along YOY'?"

Homework Equations





The Attempt at a Solution


 

Attachments

  • velocity20of20simple20harmonic20motion_0.JPG
    velocity20of20simple20harmonic20motion_0.JPG
    9.4 KB · Views: 451
Physics news on Phys.org
id like to think this is circular motion and not simple harmonic motion.

"Why the perpendicularity of vsinθ to OY makes vsinθ to have no effect along YOY'?"

It does!
 
You can represent SHM with angular velocity. Anyway, i don't see Y' in your picture.
 
Sorry, it is YO
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Bungee jump | simple harmonic motion
Replies
5
Views
2K
Velocity always aimed at rectilinearly moving particle
Replies
1
Views
1K
Rotating simple harmonic oscillator
Replies
11
Views
1K
Simple harmonic motion of charged particles
Replies
3
Views
2K
Position and acceleration in simple harmonic motion given velocity
Replies
16
Views
1K
Can you explain the correct way to choose axes for circular motion analysis?
Replies
4
Views
2K
Simple Harmonic Motion Experiment Problem
Replies
2
Views
2K
Magnitude of Frictional Force in Simple Harmonic Motion
Replies
3
Views
2K
How to derive a formula for simple harmonic motion?
Replies
1
Views
2K
Harmonic Motion of a Charged Particle
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top