Foopyblue
- 21
- 1
Homework Statement
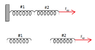
For the following arrangement of two springs, determine the effective spring constant, keff. This is the force constant of a single spring that would produce the same force on the block as the pair of springs shown for this case.
(Spring 1 is attached to Spring 2 which is attached to a block of mass m)
Solution Provided by Book:
Imagine that the block was displaced a distance x to the right of its equilibrium position. Let x1 be the distance that the first spring is stretched and let x2 be the distance that the second spring is stretched. Then x = x_1+ x_2. But x_1 = \frac {-F}{k_1} and x_2 = \frac{-F}{k_2}, so
\frac{-F}{k_1}+ \frac{-F}{k_2} = x
-F(\frac{1}{k_1}+ \frac{1}{k_2}) = x
F = \frac{1}{\frac{1}{k_1} + \frac{1}{k_2}}x
F = -\frac{k_1k_2}{k_1+k_2}x
Therefore,
keff = \frac{k_1k_2}{k_1+k_2}
Homework Equations
[/B]
F=-kx
The Attempt at a Solution
Basically I'm trying to understand how the solution they gave works. I can follow the logic up until the last line of the solution, keff = \frac{k_1k_2}{k_1+k_2}.
I understand that each spring exerts the same amount of Force. This is because as x, in F=-kx, increases, k compensates by decreasing.When I began I thought
Fnew = keff * x
I can solve for x with
x = x_1 + x_2
x_1 = \frac{-F_1}{k_1}
x_2 = \frac{-F_2}{k_2}
This leads me to
\frac{-F_1}{k_1}+ \frac{-F_2}{k_2} = x
and if you factor out the F(which you can do because the springs exert the same force) it equals
-F(\frac{1}{k_1}+ \frac{1}{k_2}) = x.
Moving it to the other side yields
F = -\frac{1}{\frac{1}{k_1} + \frac{1}{k_2}}x
And if you add the fractions they equal
F = -\frac{k_1k_2}{k_1+k_2}x
but then they set F = -\frac{k_1k_2}{k_1+k_2}x equal to Fnew = keff * x and come up with the final answer
keff = \frac{k_1k_2}{k_1+k_2}
Fnew does not equal F(The force of one spring). How can they set the equations equal to each other?
Last edited: