Understanding the Forces of a Moving Lift: T and T1

[Bandarigoda]

This is my problem,

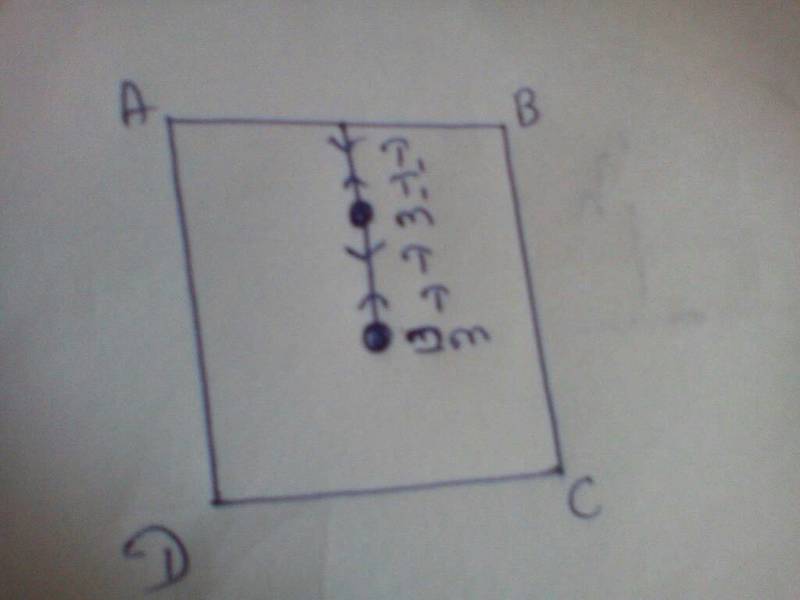
ABCD is a lift.

1-- when the lift not moving i want the T and T1.
T1= 3mg
T= 2mg
Right ?

2-- when the lift is moving with accelartion a. I want to know the new T and T1.
Are they
T1 = 3m(g+a)
T = 2m(g+a)

Am i doing it right?

 

[Simon Bridge]

Please show your reasoning.
Are the masses not equal then? I don't see that on your diagram.
You should draw separate free body diagrams for each mass.

 

[Bandarigoda]

First mass is m
Second one is 2m

 

[NascentOxygen]

That looks right. Just make sure you assign the correct +/- sign to 'a'.

 

[Bandarigoda]

That looks right. Just make sure you assign the correct +/- sign to 'a'.

Yeah, thank you sir