Hoophy
- 90
- 61
IMPORTANT!
TEXT IN GREEN HAS BEEN ADDED AND IS CORRECT
TEXT IN RED HAS BEEN REMOVED AND IS INCORRECT
1. Homework Statement
Question: An energetic father stands at the summit of a conical hill as he spins his 25 kg child around on a 5.7 kg cart with a 2.3-m-long rope.
The sides of the hill are inclined at 22∘.
He keeps the rope parallel to the ground, and friction is negligible.
What rope tension will allow the cart to spin with the 16 rpm
My variables and constants:
Child Mass = mchild = 25 kg
Cart Mass = mcart = 5.7 kg
Rope Length = L = 2.3 m
Radius = r = Lcos(22∘) = 2.3 m
Hill Grade = θ = 22∘
Angular Velocity = ω = 16 rpm = 1.67551608 rad/s
Tension = T
Total Mass = m = mchild + mcart
Centripetal Acceleration = ac
g = 9.8 m/s2
Weight = w = mg
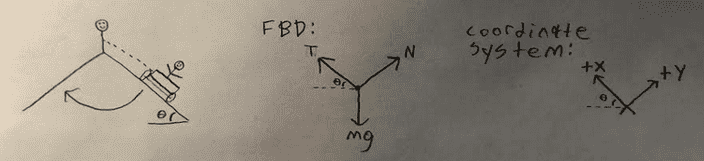
a) I drew a free body diagram with
1) Tension pointing North-West (up the slope and parallel to the surface)
2) Normal Force pointing North-East (perpendicular to the surface)
3) Weight pointing down
b) I defined my coordinate system as:
1) Positive x is up the slope and parallel to the surface
2) Positive y is parallel with the Normal Force and perpendicular to the surface (pointing away from the ground, into the sky)
c) I summed the forces in the x axis:
Fx: mac*cos(θ) = T - mg*sin(θ)
d) I isolated Tension:
T = mac*cos(θ) + mg*sin(θ)
e) I found ac:
ac = ω2r
f) I substituted ac into my equation from (d):
T = mω2r*cos(θ) + mg*sin(θ)
!) T = mω2(L*cos(θ))*cos(θ) + mg*sin(θ)
g) I plugged in known values:
T = (25 kg + 5.7 kg)(1.67551608 rad/s)2(2.3 m) + (25 kg + 5.7 kg)(9.8 m/s2)*sin(22∘)
T = (25 kg + 5.7 kg)(1.67551608 rad/s)2((2.3 m)*cos(22∘))*cos(22∘) + (25 kg + 5.7 kg)(9.8 m/s2)*sin(22∘)
h) I computed Tension as T = 310.928 N = 310 N
T = 283.111 N = 280 N
4. A note
310 N is not the correct answer, nor is 310.928 N. Also I do not know what the correct answer is...
I was wondering if someone could help me figure out what it is that I am doing incorrectly?
I really appreciate the help, thanks in advance!
Thank you so much for helping me with this problem @TSny!
TEXT IN GREEN HAS BEEN ADDED AND IS CORRECT
TEXT IN RED HAS BEEN REMOVED AND IS INCORRECT
1. Homework Statement
Question: An energetic father stands at the summit of a conical hill as he spins his 25 kg child around on a 5.7 kg cart with a 2.3-m-long rope.
The sides of the hill are inclined at 22∘.
He keeps the rope parallel to the ground, and friction is negligible.
What rope tension will allow the cart to spin with the 16 rpm
Homework Equations
My variables and constants:
Child Mass = mchild = 25 kg
Cart Mass = mcart = 5.7 kg
Rope Length = L = 2.3 m
Radius = r = Lcos(22∘) = 2.3 m
Hill Grade = θ = 22∘
Angular Velocity = ω = 16 rpm = 1.67551608 rad/s
Tension = T
Total Mass = m = mchild + mcart
Centripetal Acceleration = ac
g = 9.8 m/s2
Weight = w = mg
The Attempt at a Solution
a) I drew a free body diagram with
1) Tension pointing North-West (up the slope and parallel to the surface)
2) Normal Force pointing North-East (perpendicular to the surface)
3) Weight pointing down
b) I defined my coordinate system as:
1) Positive x is up the slope and parallel to the surface
2) Positive y is parallel with the Normal Force and perpendicular to the surface (pointing away from the ground, into the sky)
c) I summed the forces in the x axis:
Fx: mac*cos(θ) = T - mg*sin(θ)
d) I isolated Tension:
T = mac*cos(θ) + mg*sin(θ)
e) I found ac:
ac = ω2r
f) I substituted ac into my equation from (d):
T = mω2r*cos(θ) + mg*sin(θ)
!) T = mω2(L*cos(θ))*cos(θ) + mg*sin(θ)
g) I plugged in known values:
T = (25 kg + 5.7 kg)(1.67551608 rad/s)2(2.3 m) + (25 kg + 5.7 kg)(9.8 m/s2)*sin(22∘)
T = (25 kg + 5.7 kg)(1.67551608 rad/s)2((2.3 m)*cos(22∘))*cos(22∘) + (25 kg + 5.7 kg)(9.8 m/s2)*sin(22∘)
h) I computed Tension as T = 310.928 N = 310 N
T = 283.111 N = 280 N
4. A note
310 N is not the correct answer, nor is 310.928 N. Also I do not know what the correct answer is...
I was wondering if someone could help me figure out what it is that I am doing incorrectly?
I really appreciate the help, thanks in advance!
Thank you so much for helping me with this problem @TSny!
Attachments
Last edited: