Uniformly Charged Disk above a grounded conducting plane

[sweateraholic]

A uniformly charged disk has radius R. It was a charge density

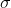and is located above the conducting plane at a distance a. The disk is parallel to the conducting plane. Find the electrostatic potential at (0,0,z) in the region above the plane. The conducting plane is grounded

 

[DeldotB]

Use the homework template - your post will most likely be deleted.
Draw out the disk and pick a point on the z axis where you want to measure the E field. Then resolve the E field into its components (some will cancell) Then use coulombs law and think how you can find Q of the ring. (Think linear charge density)