Use node-voltage method to find current, supernode problem.

[Zarathuztra]

Homework Statement

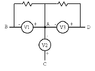
Use the node-voltage method to find i₀ in the circuit in figure if v=37V.
http://imageshack.us/a/img222/64/figurep0421.jpg

Homework Equations

The Attempt at a Solution

The hint was to use a supernode, but I'm having trouble trying to make it and get it to work, I connected the top node and bottom node with the voltage source to create the supernode. Used KCL to get 3 equations for the 3 unknowns as follows.

node A: (1/5 + 1/2)V_a + (-1/5)V_b = 0
node B: (-1/5)V_a + (1/5 + 1 + 1/5)V_b + (-1)V_c = 0
node C: (-1)V_b + (1/30 + 1)V_c = 0

solving the matrix this creates gives me V_a=V_b=V_c=0

This is definitely wrong, and I have been looking through the book (and internet) for an example and couldn't find any that was similar to this... Is my supernode location incorrect or am I making an error at a different part of the process? Thanks for help in advance.

http://imageshack.us/a/img705/8533/eeehomework04p3q.png

 

[gneill]

Hi Zarathuztra, Welcome to Physics Forums.

If you have created a supernode out of nodes A and C, then your equations should only contain one of either Va or Vc; the other potential is then referred to as either Vc+V or Va-V accordingly, where V is the voltage source that unites the nodes as a supernode.

Also, with A and C being effectively one node, that leaves only node B as an independent node (other than the chosen reference node). So you'll end up with just two node equations.

Edit: Cleaned up the text a bit; that should have been "...one of either Va or Vc", not "Va or Vb".

 

[Zarathuztra]

Hi, and Thanks :)

So basically by making the supernode it allows me to eliminate the V_c converting it to V_a-V? I'm also having trouble finding how the signs are chosen for the nodes within the closed surface that's created within the supernode, how would I know if it's a voltage rise or drop at V_a or V_c when applying KVL to the closed surface?

 

[gneill]

Hi, and Thanks :)

So basically by making the supernode it allows me to eliminate the V_c converting it to V_a-V? I'm also having trouble finding how the signs are chosen for the nodes within the closed surface that's created within the supernode, how would I know if it's a voltage rise or drop at V_a or V_c when applying KVL to the closed surface?

Supernodes contain nodes which are connected to each other by voltage sources. These voltage sources define the potential differences of the nodes, so just do a KVL "walk" from one to another and note the potential change due to the voltage sources.

Consider the following circuit fragment which might be considered as a supernode in some larger circuit.

Nodes A, B, C, D are all separated by voltage sources. That is, you can "walk" a path between any of these nodes passing only through voltage sources; going from B to D would pass through V1 and V3, for example.

Suppose you choose Node C as the reference point for this supernode. Then "walking the path" from C to B yields Vb = Vc - V2 - V1, and that's the expression you'd use in place of Vb when writing your circuit equations.

 

[The Electrician]

Not to detract from the desirability of facility with supernodes, the statement of the problem in part 1 of your first post did not indicate a reference node. Apparently the reference node chosen was your choice.

If instead you make the negative terminal of the voltage source the reference, and relabel the reference node you chose as node C, you won't have to deal with a supernode.

 

[Zarathuztra]

Supernodes contain nodes which are connected to each other by voltage sources. These voltage sources define the potential differences of the nodes, so just do a KVL "walk" from one to another and note the potential change due to the voltage sources.

Consider the following circuit fragment which might be considered as a supernode in some larger circuit.

Nodes A, B, C, D are all separated by voltage sources. That is, you can "walk" a path between any of these nodes passing only through voltage sources; going from B to D would pass through V1 and V3, for example.

Suppose you choose Node C as the reference point for this supernode. Then "walking the path" from C to B yields Vb = Vc - V2 - V1, and that's the expression you'd use in place of Vb when writing your circuit equations.

Thanks, I think that has made it clear for me, hopefully. lol.

My new Eqs are:

(1/5 + 1/2 + 1/30 + 1)V_a + (-1/5 - 1)V_b = 38.23
(-1/5 - 1)V_a + (1/5 + 1 + 1/5)V_b = -37

results: V_a= 9.25 , V_b= -18.5

@The Electrician : Thanks for that suggestion, I indeed did set the supernode and the ground, neither were given, but I ended up going that route since my professor hinted the question with, "use a supernode." So it led me to that setup.

 

[Zarathuztra]

Deleted, and posted new thread for different problem.