paraboloid
- 17
- 0
Using polar coordinates to find the volume of a bounded solid[Solved]
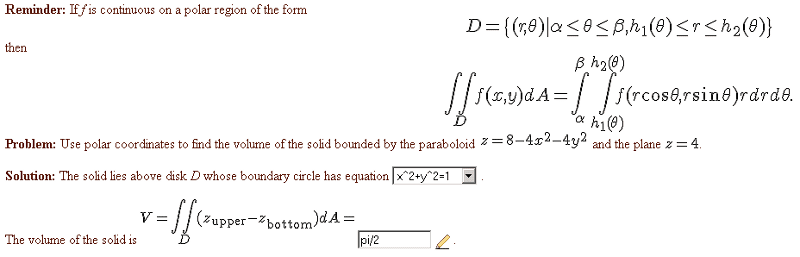
I found the equation of the boundary circle by setting z to 4 in the paraboloid.
Then I did some work to get polar coords:
x^2+y^2 = 1
x^2+y^2 = r^2
1-x^2-y^2 = 1-r^2
Then I set up my integral as such
\int_0^{2\pi}\int_{0}^{1}(1-r^2)rdrd\theta
After the double integration, I get pi/2.
edit: It should be 4r-4r3 as the integrand.
I found the equation of the boundary circle by setting z to 4 in the paraboloid.
Then I did some work to get polar coords:
x^2+y^2 = 1
x^2+y^2 = r^2
1-x^2-y^2 = 1-r^2
Then I set up my integral as such
\int_0^{2\pi}\int_{0}^{1}(1-r^2)rdrd\theta
After the double integration, I get pi/2.
edit: It should be 4r-4r3 as the integrand.
Last edited: