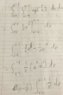Vector Calculus: Change of Variables problem

[Tom31415926535]

Homework Statement

Let D be the triangle with vertices (0,0), (1,0) and (0,1). Evaluate:

∫∫exp((y-x)/(y+x))dxdy for D

by making the substitutions u=y-x and v=y+x

Homework Equations

The Attempt at a Solution

So first I found an equation for y and x respectively:

y=(u+v)/2 and x=(v-u)/2

Then I found the Jacobian of this transformation to be 1.

Then I started solving using the terminals as:

-v<u<v and 0<v<1

However, the final solution that I got is undefined (however I can see I was on the right track. The only issue is that there was a log(0) that screwed things up)

Where have I gone wrong?

The correct answer is 1/4(e-1/e)

 

[Orodruin]

How are we going to be able to know where you went wrong when you only describe your attempt in vague terms? Please show us your actual computations including your intermediate steps.

Then I found the Jacobian of this transformation to be 1.

This is incorrect, but does not affect the whether your integral converges or not. Again, in order to have a chance at knowing how you went wrong, we need to see your intermediate steps.

 

[Tom31415926535]

You make a good point. Here are my steps

 

[Orodruin]

It would be much better and more in line with forum rules if you typed it out instead of just attaching images (see Guidelines for students and helpers, point 5). One issue is that it is impossible to quote a particular line of your computations.

Regarding the Jacobian: What is $0.5 \cdot 0.5$?

Regarding your integral: Your inner integral is not correctly done.