Vector Calculus, setting up surface area integral.

[jonathanm111]

The question goes like: find the SA of the portion S of the cone z^2 =x^2 +y^2 where z>=0 contained within the cylinder y^2+z^2<=49

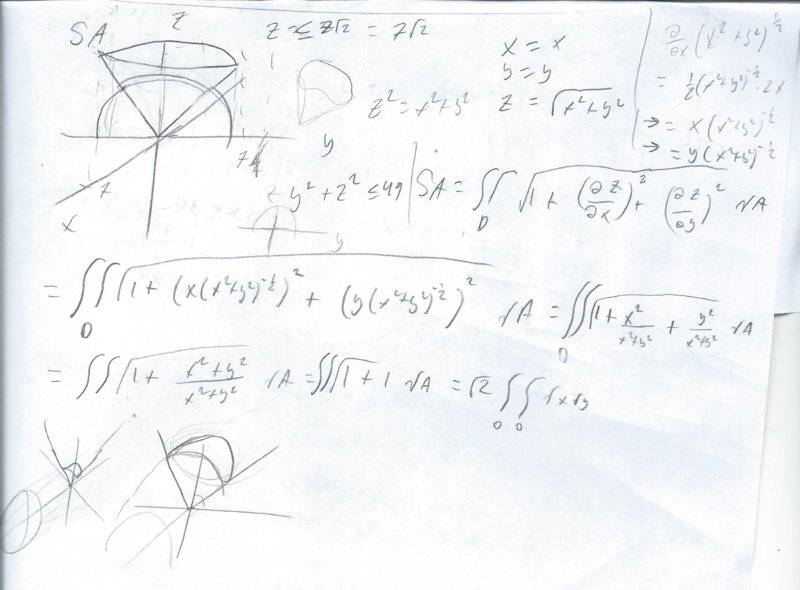
this is my attempt using the formula for SA, I could switch to parametric eqns, but even then I'd have hard time setting up limits of integration.

 

[LCKurtz]

I haven't worked it all out, but here's what I would try. The two surfaces intersect where their $z$ values are equal. So substituting $z^2$ on the cone for $z^2$ on the cylinder gives $x^2+2y^2 = 49$, or$$
\frac{x^2}{49} + \frac{y^2}{\frac{49}{2}} = 1$$This tells you if you look straight down on the surfaces, their intersection curve looks like an ellipse and, in fact, the $xy$ domain is the interior of that ellipse. So you can set it all up in the $x$ and $y$ variables and integrate over the interior of that ellipse. If you are lucky it will come out real simple, otherwise, if you have to work the integral out, you might want to change coordinates to polar like coordinates $x = 7\cos\theta,~ y = \frac 7 {\sqrt 2} \sin\theta$. Here's a sketch:

 

[jonathanm111]

I got it

you were right, polar coordinates were the way to go. this was a strange problem, professor said it wouldn't be on any tests anyways.
Thank you.

 

[LCKurtz]

Yes, it looks like you have it. But from your previous work you have $dS=\sqrt 2~dydx$ so your integral is$\iint_{ellipse}~\sqrt 2~dydx = \sqrt 2 \text{Area}$ If you know the area of an ellipse with semi-axes $a$ and $b$ is $\pi a b$ you have from the equation of the ellipse $\sqrt 2 \cdot 7 \cdot \frac 7 {\sqrt 2}=49\pi$, saving a bit of work.

 

[jonathanm111]

Yes, it looks like you have it. But from your previous work you have $dS=\sqrt 2~dydx$ so your integral is$\iint_{ellipse}~\sqrt 2~dydx = \sqrt 2 \text{Area}$ If you know the area of an ellipse with semi=axes $a$ and $b$ is $\pi a b$ you have from the equation of the ellipse $\sqrt 2 \cdot 7 \cdot \frac 7 {\sqrt 2}=49\pi$, saving a bit of work.

I believe that's how they wanted us to solve it haha. nice find