Vector circulation. Stokes, Gauss and maybe more?

In summary, the conversation discusses the relationship between the Kelvin-Stokes theorem and the Ostrogradsky/Gauss theorem. The question concerns the possibility of finding a relationship between the circulation of a vector and the volume integral, similar to how Stokes relates circulation and curl and Gauss relates flux and div. The speaker presents an idea of using a contour to enclose a volume, but is uncertain if it has been done before. They also mention the difficulty in finding a well-defined loop in a three-dimensional object.
  • #1
AlfredB
2
0
Hello. My first time posting here. So... My question is kinda hard to explain but I will try to. So we all know about the Kelvin-Stokes theorem (not talking about manifolds here) :
5f65e93751487f9350c194aa5f2bb8de.png

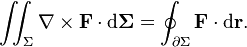
And we also know about Ostrogradsky/Gauss Theorem :
fbd758cc6576dd8296bf36e6b7403b02.png
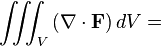[PLAIN]http://upload.wikimedia.org/wikipedia/commons/thumb/8/86/OiintLaTeX.svg/23px-OiintLaTeX.svg.png[PLAIN]http://upload.wikimedia.org/math/a/b/9/ab9fd5a4aaa36e402c98cbd36af3a70d.png

I don't have a problem with these 2. I perfectly get them. What bothers me is: can there be found a relationship between the circulation of a vector
5c8f6ef66e3c5a145a37a4e0b7219ce3.png

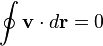
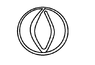
and the volume integral ? Just like Stokes relates circulation and curl and Gauss relates flux and div . Now how can a contour enclose a volume ? If you can modify is shape you can(see my attachment ) THat's just an idea, I don't know if it's been done or it can be done. And while you can modifiy the shape of the contour to get different surfaces of different areas you can only get one sphere of only one volume, speciffic to the length of the contour. I'm sorry if I was inchorent, just ask me if you want me to try and formulate my question in a different way although I tried to explain it as good as I could.
 

Attachments

  • 1.png
    1.png
    2.9 KB · Views: 475
Last edited by a moderator:
Physics news on Phys.org
  • #2
Circulation about what loop? A three dimensional object may have a well defined two dimensional surface but there are infinitely many one dimensional loops lying in that surface. (I'm not clear what you picture is supposed to show but it is certainly not a curve completely covering the sphere.)
 

FAQ: Vector circulation. Stokes, Gauss and maybe more?

What is vector circulation?

Vector circulation is a mathematical concept that describes the flow of a vector field around a closed curve. It is represented by the line integral of the vector field over the closed curve and is a measure of the tendency of a vector field to rotate around a given point.

What is Stokes' theorem?

Stokes' theorem is a fundamental theorem in vector calculus that relates the line integral of a vector field around a closed curve to the surface integral of the curl of the vector field over the surface bounded by the curve. It is a generalization of the fundamental theorem of calculus and has many important applications in physics and engineering.

How is vector circulation related to fluid dynamics?

In fluid dynamics, vector circulation is used to describe the motion and behavior of fluids. It is related to the concept of vorticity, which is a measure of the local rotation of a fluid element. Vector circulation is often used to calculate the lift force on an object in a fluid, such as an airplane wing, and is a crucial concept in understanding the dynamics of fluid flow.

What is the significance of Gauss' theorem?

Gauss' theorem, also known as the divergence theorem, is a fundamental theorem in vector calculus that relates the flux of a vector field through a closed surface to the volume integral of the divergence of the vector field over the region enclosed by the surface. It is a key tool in solving many physical problems involving vector fields, such as calculating electric or magnetic fields.

How are Stokes' and Gauss' theorems related?

Stokes' and Gauss' theorems are related through the concept of the curl of a vector field. Stokes' theorem states that the line integral of a vector field around a closed curve is equal to the surface integral of the curl of the vector field over the surface bounded by the curve. Gauss' theorem states that the flux of a vector field through a closed surface is equal to the volume integral of the divergence of the vector field over the region enclosed by the surface. These theorems are complementary and are often used together in solving physical problems.

Similar threads

I Stokes Theorem: Vector Integral Identity Proof
Replies
2
Views
2K
Don't understand Stoke's Theorem (Revised)
Replies
3
Views
3K
I Why is Stoke's theorem of a closed path equal to zero?
Replies
9
Views
11K
I What do Stokes' and Green's theorems represent?
Replies
7
Views
2K
Meaning of Curl from stokes' theorem
Replies
3
Views
2K
I Conditions for applying Gauss' Law
Replies
1
Views
475
Does Gauss' Law use line integrals or surface integrals?
Replies
2
Views
2K
I Sign mistake when computing integral with differential forms
Replies
3
Views
2K
What is the one-dimensional counterpart to the Green-Gauss theorem?
Replies
28
Views
1K
Understanding Greene's, Stoke's, and the Divergence theorems
Replies
4
Views
6K

Hot Threads

Recent Insights

Back
Top